题目内容
如图，一个等边三角形，一个直角三角形以及一个等腰三角形如图放置，已知等腰三角形的底角∠3=64°，则∠1+∠2=考点：等边三角形的性质,等腰三角形的性质
专题：
分析：如图，由等边三角形和直角三角形可得∠1+α=120°，∠2+β=90°，且∠3=α+β，可求得∠1+∠2．
解答：
解：如图，由等边三角形和直角三角形可得∠1+α=120°，∠2+β=90°，
∴∠1+∠2+α+β=90°+120°=210°，
且∠3=α+β，
∴α+β=64°，
∴∠1+∠2=210°-64°=146°，
故答案为：146°．
解：如图，由等边三角形和直角三角形可得∠1+α=120°，∠2+β=90°，∴∠1+∠2+α+β=90°+120°=210°，
且∠3=α+β，
∴α+β=64°，
∴∠1+∠2=210°-64°=146°，
故答案为：146°．
点评：本题主要考查等边三角形的性质及外角的性质，由条件利用α、β得到∠3和∠1、∠2之间的关系是解题的关键
练习册系列答案
相关题目
甲乙两台机床同时生产一种零件，在5天内，两台机床每天生产的次品数分别如下：
甲：3，2，1，1，3；
乙：2，2，3，3，0．
计算两台机床数据的方差，并从结果中分析在这5天中哪台机床生产的次品数波动较小．
甲：3，2，1，1，3；
乙：2，2，3，3，0．
计算两台机床数据的方差，并从结果中分析在这5天中哪台机床生产的次品数波动较小．
在Rt△ABC中，已知∠A=52°，b=12，则a的值约等于（ ）
| A、15.36 |
| B、16.35 |
| C、17.34 |
| D、18.35 |
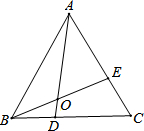如图，点D，E分别在等边△ABC的BC，CA边上，连接AD，BE相交于点O，且∠BOD=60°．
如图，已知四点A，B，C，D，按要求在图上完成下面的问题：