题目内容
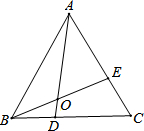 如图,点D,E分别在等边△ABC的BC,CA边上,连接AD,BE相交于点O,且∠BOD=60°.
如图,点D,E分别在等边△ABC的BC,CA边上,连接AD,BE相交于点O,且∠BOD=60°.(1)求证:BD=CE;
(2)若将题中的点D,E分别移到BC,CA的延长线,直线AD,BE交于点O,且∠BOD=60°,是否仍能得到BD=CE?请你作出判断,并说明理由.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)易证∠BDO=∠BEC,即可证明△ABD≌△BCE,即可解题;
(2)成立,易证∠E=∠D,进而可以证明△ACD≌△BAE,可得AE=CD,即可解题.
(2)成立,易证∠E=∠D,进而可以证明△ACD≌△BAE,可得AE=CD,即可解题.
解答:解:(1)∵∠BOD=60°,∠C=60°,∠OBD=∠CBE,
∴∠BDO=∠BEC,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(AAS),
∴BD=CE;
(2)成立;
证明:画出图形,

∵∠BOD=60°,
∴∠AOE=120°,
∵∠OAE=∠CAD,∠ACD=∠AOE=120°,
∴∠E=∠D,
在△ACD和△BAE中,
,
∴△ACD≌△BAE(AAS),
∴AE=CD,
∵BC=AC,
∴CE=BD.
∴∠BDO=∠BEC,
在△ABD和△BCE中,
|
∴△ABD≌△BCE(AAS),
∴BD=CE;
(2)成立;
证明:画出图形,

∵∠BOD=60°,
∴∠AOE=120°,
∵∠OAE=∠CAD,∠ACD=∠AOE=120°,
∴∠E=∠D,
在△ACD和△BAE中,
|
∴△ACD≌△BAE(AAS),
∴AE=CD,
∵BC=AC,
∴CE=BD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中(1)求证△ACD≌△BAE、(2)中求证△ACD≌△BAE是解题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 如图,一个等边三角形,一个直角三角形以及一个等腰三角形如图放置,已知等腰三角形的底角∠3=64°,则∠1+∠2=
如图,一个等边三角形,一个直角三角形以及一个等腰三角形如图放置,已知等腰三角形的底角∠3=64°,则∠1+∠2=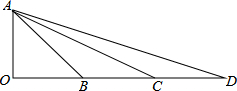 如图,∠AOD=90°,OA=OB=BC=CD,∠BAC=20°,求∠D的度数.
如图,∠AOD=90°,OA=OB=BC=CD,∠BAC=20°,求∠D的度数.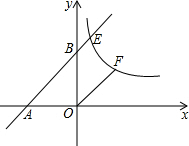 如图,直线y=x+3与x轴、y轴交于A、B两点,与双曲线y=
如图,直线y=x+3与x轴、y轴交于A、B两点,与双曲线y=