Question

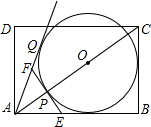矩形ABCD中，BC=6，AB=8，E是AB上一点，AE的长为，把矩形沿对角线AC对折，点E的对应点为F，EF与AC交于点Q，以CP为直径的⊙O与直线AQ相切于点Q．
（1）用含t的代数式表示AP、PE的长；
（2）求t的值．

Answer 1

考点：切线的性质,矩形的性质

专题：计算题

分析：（1）在Rt△ABC中利用勾股定理计算出AC=10，再根据折叠的性质得到EF⊥AC，则可证明Rt△APE∽Rt△ABC，利用相似比得到

AP

8

=

PE

6

=

t

10

，然后根据比例的性质易得AP=

4

5

t，PE=

3

5

t；
（2）连结OQ，作OM⊥AB于M，ON⊥BC于N，如图，由CP为⊙O的直径，OP⊥EF可判断EF为⊙O的切线，根据切线的性质，由直线AQ与⊙O相切于点Q得到OQ⊥AQ，再利用折叠的性质得∠BAC=∠QAC，根据角平分线定理得到OM=OQ，于是可判断AB与⊙O相切，根据切线长定理得EM=PE=

3

5

t；接着利用切线的性质得ON=OM，则可判断四边形BMON为正方形，得到BM=OM，然后证明△AOM∽△ACB，利用相似比得到OM=

6

5

t，则BM=

6

5

t，再利用AE+EM+BM=AB得到t+

3

5

t+

6

5

t=8，最后解一次方程即可．

解答：解：（1）在Rt△ABC中，∵BC=6，AB=8，
∴AC=

AB2+BC2

=10，
∵矩形沿对角线AC对折，点E的对应点为F，
∴EF⊥AC，
∵∠EAP=∠CAB，
∴Rt△APE∽Rt△ABC，
∴

AP

AB

=

PE

BC

=

AE

AC

，即

AP

8

=

PE

6

=

t

10

，
∴AP=

4

5

t，PE=

3

5

t；
（2）连结OQ，作OM⊥AB于M，ON⊥BC于N，如图，
∵CP为⊙O的直径，OP⊥EF，
∴EF为⊙O的切线，
∵直线AQ与⊙O相切于点Q，
∴OQ⊥AQ，
∵矩形沿对角线AC对折，
∴∠BAC=∠QAC，即AC平分∠BAQ，
∴OM=OQ，
∴AB与⊙O相切，
∴EM=PE=

3

5

t，
∵BC与⊙O相切，
∴ON=OM，
∴四边形BMON为正方形，
∴BM=OM，
∵OM∥BC，
∴△AOM∽△ACB，
∴

OM

BC

=

AM

AB

，即

OM

6

=

t+ 3 5 t

8

，解得OM=

6

5

t，
∴BM=

6

5

t，
∵AE+EM+BM=AB，
∴t+

3

5

t+

6

5

t=8，
∴t=

20

7

．

点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了相似三角形的判定与性质、矩形的性质和折叠的性质．