题目内容
如图，△ABC≌△ADE，∠EAC=35°，则∠BAD=考点：全等三角形的性质
专题：
分析：根据全等三角形性质得出∠BAC=∠DAE，求出∠BAD=∠EAC，代入求出即可．
解答：解：∵△ABC≌△ADE，
∴∠BAC=∠DAE，
∴∠BAC-∠DAC=∠DAE-∠DAC，
∴∠BAD=∠EAC，
∵∠EAC=35°，
∴∠BAD=35°，
故答案为：35．
∴∠BAC=∠DAE，
∴∠BAC-∠DAC=∠DAE-∠DAC，
∴∠BAD=∠EAC，
∵∠EAC=35°，
∴∠BAD=35°，
故答案为：35．
点评：本题考查了全等三角形性质的应用，注意：全等三角形的对应边相等，对应角相等．
练习册系列答案
相关题目
已知一不透明的正方体的六个面上分别写着1至6六个数字，如图是我们能看到的三种情况，那么2的对面数字是
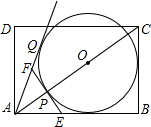矩形ABCD中，BC=6，AB=8，E是AB上一点，AE的长为，把矩形沿对角线AC对折，点E的对应点为F，EF与AC交于点Q，以CP为直径的⊙O与直线AQ相切于点Q．
如图，A城气象台测得台风中心在A城正西方向78的B处，以每小时20的速度沿BC方向移动，A到BC的距离AD=30，在距台风中心50的圆形区域都将受到台风的影响．
如图所示的抛物线二次函数y=ax2-3x+a2-a-2的图象，那么a的值是