题目内容
计算:1002+992-982+972-…-62+52-42+32-22+12.
考点:因式分解-运用公式法
专题:
分析:分组使用平方差公式,再利用自然数求和公式解题.
解答:解:原式=(12-22)+(32-42)+…+(992-1002)
=(1-2)(1+2)+(3-4)(3+4)+…+(97-98)(97+98)+1002+992
=-(1+2)-(3+4)-…-(97+98)+1002+992
=-(1+2+3+4+…+98)+1002+992
=-4851+1002+992
=-14950.
=(1-2)(1+2)+(3-4)(3+4)+…+(97-98)(97+98)+1002+992
=-(1+2)-(3+4)-…-(97+98)+1002+992
=-(1+2+3+4+…+98)+1002+992
=-4851+1002+992
=-14950.
点评:本题考查了平方差公式的运用,注意分组后两数的差都为-1,所有两数的和组成自然数求和.

练习册系列答案
相关题目
已知关于x的方程x2+px-15=0的两根之差的绝对值是8,则P的值是( )
| A、±2 | ||
| B、2 | ||
| C、-2 | ||
D、±
|
某地区2010年投入教育经费2500万元,预计到2012年共投入8000万元.设这两年投入教育经费的年平均增长率为x,则下列方程正确的是( )
| A、2500+2500(1+x)+2500(1+x)2=8000 |
| B、2500x2=8000 |
| C、2500(1+x)2=8000 |
| D、2500(1+x)+2500(1+x)2=8000 |
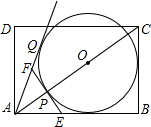 矩形ABCD中,BC=6,AB=8,E是AB上一点,AE的长为,把矩形沿对角线AC对折,点E的对应点为F,EF与AC交于点Q,以CP为直径的⊙O与直线AQ相切于点Q.
矩形ABCD中,BC=6,AB=8,E是AB上一点,AE的长为,把矩形沿对角线AC对折,点E的对应点为F,EF与AC交于点Q,以CP为直径的⊙O与直线AQ相切于点Q.