题目内容
3.已知:a=$\frac{1}{2+\sqrt{3}}$,b=$\frac{1}{2-\sqrt{3}}$,求下列各式的值.(1)$\frac{1}{a+1}$+$\frac{1}{b+1}$;
(2)a2-ab+b2;
(3)a2b+ab2.
分析 首先化简a=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$,b=$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$,
(1)直接代入计算即可;
(2)整理a2-ab+b2=(a-b)2+ab代入求得数值即可;
(3)整理a2b+ab2=ab(a+b)代入求得数值即可.
解答 解:∵a=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$,b=$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$,
∴(1)原式=$\frac{1}{3-\sqrt{3}}$+$\frac{1}{3+\sqrt{3}}$=$\frac{3+\sqrt{3}}{6}$+$\frac{3-\sqrt{3}}{6}$=1;
(2)原式=(a-b)2+ab=12+1=13;
(3)原式=ab(a+b)=4.
点评 此题考查二次根式的化简求值,注意先化简,再进一步代入求得数值.

练习册系列答案
相关题目
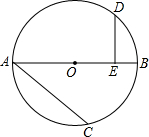 如图,已知AB为⊙O的直径,D、C为⊙O上两点,弧AD=弧DC,连结AC.过点D作DE⊥0B于E.求证:DE=$\frac{1}{2}$AC.
如图,已知AB为⊙O的直径,D、C为⊙O上两点,弧AD=弧DC,连结AC.过点D作DE⊥0B于E.求证:DE=$\frac{1}{2}$AC.