题目内容
11. 如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.(1)求BD的长;
(2)在直线AC的同侧,以点O为位似中心,作出△CON的位似三角形,并使△CON与和它位似的三角形的位似比是1:2.(写出结果,不写作法,保留作图痕迹).
分析 (1)根据平行四边形的性质得AD∥BC,AD=BC,OB=OD,则利用DM∥BC可判断△MND∽△CNB,所以MD:BC=DN:BN=1:2,设OB=OD=x,则BD=2x,BN=OB+ON=x+1,DN=x-1,于是得到x+1=2(x-1),解得x=3,所以BD=2x=6;
(2)如图,在OD上截取NG=ON,延长OC到H,使HC=OC,则△HOG满足条件.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OB=OD,
∴DM∥BC,
∴△MND∽△CNB,
∴MD:BC=DN:BN,
∵M为AD中点,
∴MD:BC=1:2,
∴DN:BN=1:2,即BN=2DN,
设OB=OD=x,则BD=2x,BN=OB+ON=x+1,DN=x-1,
∴x+1=2(x-1),解得x=3,
∴BD=2x=6;
(2)如图,△HOG为所作.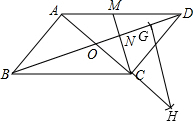
点评 本题考查了作图-位似变换:先确定位似中心;②分别连接并延长位似中心和能代表原图的关键点;再根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了平行四边形的性质.

练习册系列答案
相关题目
2.若A(3,y1),B(2,y2)在函数$y=\frac{2}{x}$的图象上,则y1,y2大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
6.下列根式是最简二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{{x}^{2}-1}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{{a}^{3}b}$ |
3. 有理数a,b,c在数轴上的位置如图所示,则|a+c|-|c-b|-|a+b|=( )
有理数a,b,c在数轴上的位置如图所示,则|a+c|-|c-b|-|a+b|=( )
 有理数a,b,c在数轴上的位置如图所示,则|a+c|-|c-b|-|a+b|=( )
有理数a,b,c在数轴上的位置如图所示,则|a+c|-|c-b|-|a+b|=( )| A. | 0 | B. | 2a+2b | C. | -2a-2c | D. | 2b-2c |
1.若直角三角形的三边长分别为6、10、m,则m2的值为( )
| A. | 8 | B. | 64 | C. | 136 | D. | 136或64 |
 如图所示,在△ABC中,AB=AC,∠B=30°,D为BC上一点,且∠DAB=45°
如图所示,在△ABC中,AB=AC,∠B=30°,D为BC上一点,且∠DAB=45°