题目内容
7.计算:(1)$\sqrt{18a}$•$\sqrt{2a}$(a≥0);
(2)$\sqrt{8}$+3$\sqrt{\frac{1}{3}}$-$\frac{1}{{\sqrt{2}}}$+$\frac{{\sqrt{3}}}{2}$;
(3)($\frac{{\sqrt{8}}}{2}$-$\sqrt{\frac{2}{5}}}$)(5$\sqrt{\frac{1}{2}}$-$\frac{1}{{\sqrt{5}}}}$).
分析 (1)根据二次根式的乘法法则运算;
(2)先把各二次根式化简为最简二次根式,然后合并即可;
(3)先把各二次根式化简为最简二次根式,然后利用乘法公式展开,再化简即可.
解答 解:(1)原式=$\sqrt{18a•2a}$
=6a;
(2)原式=2$\sqrt{2}$+$\sqrt{3}$-$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$
=$\frac{3\sqrt{2}}{2}$+$\frac{3\sqrt{3}}{2}$;
(3)原式=($\sqrt{2}$-$\frac{\sqrt{10}}{5}$)($\frac{5\sqrt{2}}{2}$-$\frac{\sqrt{5}}{5}$)
=5-$\frac{\sqrt{10}}{5}$-$\sqrt{5}$-$\frac{\sqrt{2}}{5}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
19.已知圆锥的底面半径为5,母线长为8,则这个圆锥的侧面积是( )
| A. | 13π | B. | 20π | C. | 40π | D. | 200π |
 如图,在⊙O中,半径OC⊥AB于点D,连结BC.
如图,在⊙O中,半径OC⊥AB于点D,连结BC.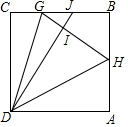 正方形ABCD中,∠GDH=45°,DI⊥GH并延长交BC于点J,GJ=5,GH=I0,求DJ长.
正方形ABCD中,∠GDH=45°,DI⊥GH并延长交BC于点J,GJ=5,GH=I0,求DJ长.