题目内容
抛物线y=-x2-mx+m+2与x轴有两个交点A、B,顶点C,求△ABC面积的最小值.
考点:抛物线与x轴的交点
专题:计算题
分析:先把解析式配成顶点式得到顶点C的坐标为(-
,
),再利用抛物线与x轴两交点之间的距离公式计算出AB=
,接着根据三角形面积公式得到△ABC的面积=
•
•
,变形得到△ABC的面积=
•
,然后利用非负数的性质求△ABC面积的最小值.
| m |
| 2 |
| m2+4m+8 |
| 4 |
| m2+4m+8 |
| 1 |
| 2 |
| m2+4m+8 |
| m2+4m+8 |
| 4 |
| 1 |
| 8 |
| (m2+4m+8)3 |
解答:解:∵y=-x2-mx+m+2=-(x+
)2+
,
∴顶点C的坐标为(-
,
),
∵AB=
=
,
∴△ABC的面积=
•
•
=
•
=
,
∵(m+2)2≥0,
∴当m=-2时,△ABC的面积最小,最小值为
•
=1.
| m |
| 2 |
| m2+4m+8 |
| 4 |
∴顶点C的坐标为(-
| m |
| 2 |
| m2+4m+8 |
| 4 |
∵AB=
| ||
| |-1| |
| m2+4m+8 |
∴△ABC的面积=
| 1 |
| 2 |
| m2+4m+8 |
| m2+4m+8 |
| 4 |
=
| 1 |
| 8 |
| (m2+4m+8)3 |
=
| 1 |
| 8 |
| [(m+2)2+4]3 |
∵(m+2)2≥0,
∴当m=-2时,△ABC的面积最小,最小值为
| 1 |
| 8 |
| 64 |
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
在-0.101001,
,
,-
,0中,无理数的个数是( )
| 7 |
| 1 |
| 4 |
| π |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列说法正确的是( )
| A、相切两圆的连心线经过切点 |
| B、长度相等的两条弧是等弧 |
| C、平分弦的直径垂直于弦 |
| D、相等的圆心角所对的弦相等 |
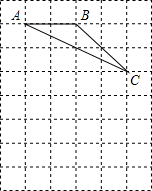 如图,在8×6的正方形网格中,△ABC的顶点都在边长为1的小正方形的顶点上.
如图,在8×6的正方形网格中,△ABC的顶点都在边长为1的小正方形的顶点上.
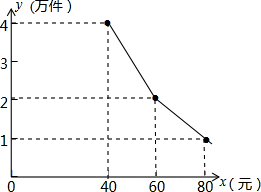 为扶持大学生自主创业,市政府提供了80万元无息贷款,用于大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司经营的利润偿逐步还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
为扶持大学生自主创业,市政府提供了80万元无息贷款,用于大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司经营的利润偿逐步还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.