题目内容
抛物线y=x2-
x+
(其中n是正整数)与x轴交于An、Bn两点,若以AnBn表示这两点间的距离,则A1B1= ;A1B1+A2B2= ;A1B1+A2B2+A3B3+…+AnBn= .(用含n的代数式表示)
| 2n+1 |
| n(n+1) |
| 1 |
| n(n+1) |
考点:抛物线与x轴的交点
专题:规律型
分析:先化简抛物线y=x2-
x+
,然后求出一元二次方程的根,根据两点间的坐标差求出距离,找出规律解答即可.
| 2n+1 |
| n(n+1) |
| 1 |
| n(n+1) |
解答:解:y=x2-
x+
=(x-
)(x-
)
故抛物线与x轴交点坐标为(
,0)和(
,0)
由题意,AnBn=
-
.
所以 A1B1=1-
=
,
A1B1+A2B2=(1-
)+(
-
)=
+
=
A1B1+A2B2+A3B3+…+AnBn═(1-
)+(
-
)+…+(
-
)
=1-
=
.
故答案是:
;
;
.
| 2n+1 |
| n(n+1) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
故抛物线与x轴交点坐标为(
| 1 |
| n |
| 1 |
| n+1 |
由题意,AnBn=
| 1 |
| n |
| 1 |
| n+1 |
所以 A1B1=1-
| 1 |
| 2 |
| 1 |
| 2 |
A1B1+A2B2=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
A1B1+A2B2+A3B3+…+AnBn═(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
故答案是:
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
点评:本题考查的是二次函数与一元二次方程,在解答过程中,注意二次函数与一元二次方程之间的联系,并从中择取有用信息解题;求两点间的距离时,要利用两点间的坐标差来解答.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
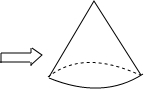 如图,现有一个半径为8cm的半圆形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),该圆锥的高为( )
如图,现有一个半径为8cm的半圆形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),该圆锥的高为( )| A、2cm | ||
B、2
| ||
| C、4cm | ||
D、4
|
 如图,已知点C在点B的北偏西65°方向,点B在点A的北偏东35°方向,则∠ABC的度数为( )
如图,已知点C在点B的北偏西65°方向,点B在点A的北偏东35°方向,则∠ABC的度数为( )| A、65° | B、35° |
| C、80° | D、70° |
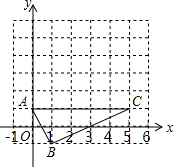 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1).
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1). 某公司销售一种市场需求较大的新型产品,每件行星新型产品的进阶为40元,公司要求售价不低于进价,但不高于65元,通过作市场调查,得到数据如图表所示:
某公司销售一种市场需求较大的新型产品,每件行星新型产品的进阶为40元,公司要求售价不低于进价,但不高于65元,通过作市场调查,得到数据如图表所示:
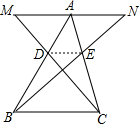 如图,MN经过△ABC的顶点A,MN∥BC,AM=AN,MC交AB于E.
如图,MN经过△ABC的顶点A,MN∥BC,AM=AN,MC交AB于E.