Question

15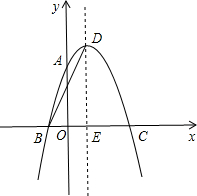．如图；抛物线y=ax²+2x+c过点A（0，3），B（-1，0），请回答下列问题：
（1）求抛物线的解析式；
（2）抛物线的顶点为D，对称轴与x轴交于点E，连接BD，求BD的长．

Answer 1

分析 （1）把点A（0，3），B（-1，0）代入y=ax²+2x+c利用待定系数法即可求得；
（2）把抛物线的一般式化成顶点式，求得顶点坐标，然后根据勾股定理即可求得BD的长．

解答 解：（1）把点A（0，3），B（-1，0）代入y=ax²+2x+c得$\left\{\begin{array}{l}{c=3}\\{a-2+c=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=-1}\\{c=3}\end{array}\right.$，
∴抛物线的解析式为y=-x²+2x+3；
（2）由y=-x²+2x+3=-（x-1）²+4，
∴顶点坐标为（1，4），
∵B（-1，0），
∴BD=$\sqrt{（1+1）^{2}+（4-0）^{2}}$=2$\sqrt{5}$．

点评 本题考查了待定系数法求二次函数的解析式和勾股定理的应用，求得顶点坐标是本题的关键．