题目内容
扇形OAB的弦AB=18,半径为6的圆D恰与OA、OB和弧AB相切,则圆O的半径为________.
18
分析:连接OD并延长交AB于点E,根据内切圆的性质可得OE⊥AB,再根据垂径定理求出AE,设⊙O的半径为r,用r表示出OD,然后根据△ODF和△OAE相似,利用相似三角形对应边成比例列式求解即可.
解答: 解:如图,连接OD并延长交AB于点E,
解:如图,连接OD并延长交AB于点E,
∵⊙D与弧AB相切,
∴OE⊥AB,
∵AB=18,
∴AE= AB=9,
AB=9,
设⊙O的半径为r,
∵⊙D的半径为6,⊙D与弧AB相切,
∴OD=r-6,
∵⊙D与OA、OB相切,
∴OF⊥OA,
∴△ODF∽△OAE,
∴ =
=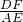 ,
,
即 =
=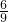 ,
,
解得r=18,
即圆O的半径为18.
故答案为:18.
点评:本题考查了垂径定理的应用,考查了切线的定义,考查了正方形各边长相等的性质,考查了全等三角形对应边相等的性质,本题中根据BO=BF+FO求BO的值是解题的关键.
分析:连接OD并延长交AB于点E,根据内切圆的性质可得OE⊥AB,再根据垂径定理求出AE,设⊙O的半径为r,用r表示出OD,然后根据△ODF和△OAE相似,利用相似三角形对应边成比例列式求解即可.
解答:
 解:如图,连接OD并延长交AB于点E,
解:如图,连接OD并延长交AB于点E,∵⊙D与弧AB相切,
∴OE⊥AB,
∵AB=18,
∴AE=
 AB=9,
AB=9,设⊙O的半径为r,
∵⊙D的半径为6,⊙D与弧AB相切,
∴OD=r-6,
∵⊙D与OA、OB相切,
∴OF⊥OA,
∴△ODF∽△OAE,
∴
 =
=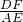 ,
,即
 =
=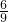 ,
,解得r=18,
即圆O的半径为18.
故答案为:18.
点评:本题考查了垂径定理的应用,考查了切线的定义,考查了正方形各边长相等的性质,考查了全等三角形对应边相等的性质,本题中根据BO=BF+FO求BO的值是解题的关键.

练习册系列答案
相关题目
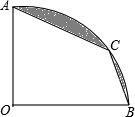 扇形OAB的半径OA=1,圆心角∠AOB=90°,点C是弧AB上的动点,连结AC和BC,记弦AC、CB与弧AC、CB围成的阴影部分的面积为S,则S的最小值为( )
扇形OAB的半径OA=1,圆心角∠AOB=90°,点C是弧AB上的动点,连结AC和BC,记弦AC、CB与弧AC、CB围成的阴影部分的面积为S,则S的最小值为( )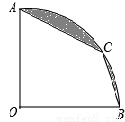
 B.
B.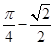 C.
C.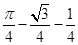 D.
D.