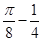题目内容
8、扇形OAB的弦AB=18,半径为6的圆D恰与OA、OB和弧AB相切,则圆O的半径为
15
.分析:根据切线的性质可以求得四边形OFDG为正方形、△DBE≌△DBF,可得BF=BE,OF=DF=6,根据切线和垂径定理可求得BO的长,即可解题.
解答:解:DE=DF=DG=6,AE=EB=9,
由切线的性质可知四边形OFDG为正方形,
∴OF=DF=6,
∵△DBE≌△DBF,
且由垂径定理可得BE=BF=9,
∴BO=9+6=15,
故答案为 15.

由切线的性质可知四边形OFDG为正方形,
∴OF=DF=6,
∵△DBE≌△DBF,
且由垂径定理可得BE=BF=9,
∴BO=9+6=15,
故答案为 15.

点评:本题考查了垂径定理的应用,考查了切线的定义,考查了正方形各边长相等的性质,考查了全等三角形对应边相等的性质,本题中根据BO=BF+FO求BO的值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
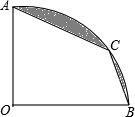 扇形OAB的半径OA=1,圆心角∠AOB=90°,点C是弧AB上的动点,连结AC和BC,记弦AC、CB与弧AC、CB围成的阴影部分的面积为S,则S的最小值为( )
扇形OAB的半径OA=1,圆心角∠AOB=90°,点C是弧AB上的动点,连结AC和BC,记弦AC、CB与弧AC、CB围成的阴影部分的面积为S,则S的最小值为( )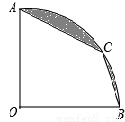
 B.
B.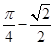 C.
C.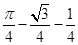 D.
D.