题目内容
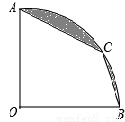
扇形OAB的半径OA=1,圆心角∠AOB=90°,点C是弧AB上的动点,连结AC和BC,记弦AC,CB与弧AC、CB围成的阴影部分的面积为S,则S的最小值为( )
A. B.
B.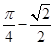 C.
C.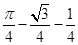 D.
D.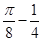
【答案】
B.
【解析】
试题分析:如图,连接AB, 要使阴影部分的面积最小,就需要满足四边形AOBC的面积最大,只需满足△ABC的面积最大即可,从而可得当点C位于弧AB的中点时,△ABC的面积最大.
取 的中点C',连接OC',OC'与AB相交于点D,
的中点C',连接OC',OC'与AB相交于点D,
则OC'⊥AB,AB= ,OD=
,OD= AB=
AB= ,
, ,
,
∴ .
.
∴S的最小值为= .
.
故选B.

考点:1.动点问题;2. 等腰直角三角形的性质;3.勾股定理;4.垂径定理;5.扇形和三角形面积;6.转换思想的应用.

练习册系列答案
相关题目

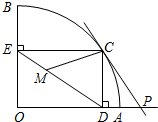
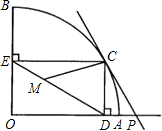 点D,作CE⊥OB于点E,点M在DE上,DM=2EM,过点C的直线PC交OA的延长线于点P,且∠CPD=∠CDE.
点D,作CE⊥OB于点E,点M在DE上,DM=2EM,过点C的直线PC交OA的延长线于点P,且∠CPD=∠CDE.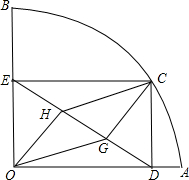 如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是
如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是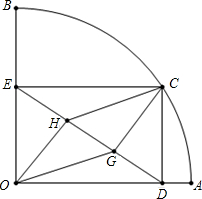 如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是
如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是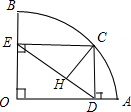 如图,扇形OAB的半径OA=6,圆心角∠AOB=90°,C是
如图,扇形OAB的半径OA=6,圆心角∠AOB=90°,C是
 如图,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是
如图,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是