题目内容
5.如图1,△ABC的两条中线AD、BE相交于点O(1)求证:DO:AO=1:2;
(2)连接CO并延长交AB于F,求证:CF也是△ABC的中线;
(3)在(2)中,若∠A=90°,其它条件不变,连接DF交BE于K(如图2),连接ED,且△EDK∽△CAB,求AC:AB的值.

分析 (1)连接ED,可得ED为三角形ABC的中位线,利用中位线定理得到ED与AB平行,且等于AB的一半,进而得到三角形EOD与三角形AOB相似,且相似比为1:2,即可得证;
(2)设ED与CF交于点G,由三角形GOD与三角形AFO相似,由相似得比例,再由DG与AB平行,得比例,确定出AF=BF,即可得证;
(3)由∠A为直角,得到四边形AFDE为矩形,可得出三角形EDK与三角形BAE相似,再由三角形EDK与三角形CAB相似,得到三角形BAE与三角形CAB相似,由相似得比例,求出所求之比即可.
解答 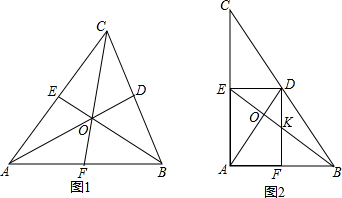 (1)证明:连接ED,
(1)证明:连接ED,
∵E、D分别为AC、BC的中点,
∴ED∥AB,且ED=$\frac{1}{2}$AB,
∴△EDO∽△BAO,
∴DO:AO=ED:AB=1:2;
(2)证明:设CF交ED于点G,
由△DGO∽△AFO,得到DG:AF=DO:AO=1:2,
由DG∥AB得DG:BF=CD:CB=1:2,
∴DG:AF=DG:BF,
∴AF=BF,
∴AF也是△ABC的中线;
(3)解:由∠A=90°,得到四边形AFDE是矩形,
∴△EDK∽△BAE,
∵△EDK∽△CAB,
∴△BAE∽△CAB,
∴AE:AB=AB:AC,
∵AE=$\frac{1}{2}$AC,
∴AC:AB=$\sqrt{2}$.
点评 此题属于相似形综合题,涉及的知识有:相似三角形的判定与性质,三角形中位线定理,矩形的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15.下列调查适合抽样调查的是( )
| A. | 对某社区的卫生死角进行调查 | |
| B. | 对七年级(1)班40名同学的身高情况进行调查 | |
| C. | 审核书稿中的错别字 | |
| D. | 对中学生目前的睡眠情况进行调查 |
 如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴.直线OB于点E、F,点E为垂足,连结CF.
如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴.直线OB于点E、F,点E为垂足,连结CF. 在图中沿正方形的网格线把这个图形分割成两个全等形.你有几种不同的分割方法?
在图中沿正方形的网格线把这个图形分割成两个全等形.你有几种不同的分割方法? 如图是某校舞蹈队成员的年龄分布条形统计图,则他们年龄的中位数是15.5岁.
如图是某校舞蹈队成员的年龄分布条形统计图,则他们年龄的中位数是15.5岁.