题目内容
 已知,如图,点B、E、F、C在同一直线上,∠B=∠C,BE=CF,要说明△ABF≌△DCE,还要添加的条件为
已知,如图,点B、E、F、C在同一直线上,∠B=∠C,BE=CF,要说明△ABF≌△DCE,还要添加的条件为考点:全等三角形的判定
专题:开放型
分析:已知一边、一角对应相等,可再加第二组角对应相等或已知两组边的夹角相等都可以.
解答:解:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE.
①由条件可再添加AB=DC,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(SAS),
②可添加∠AFB=∠DEC,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(ASA),
故答案为:AB=DC(或∠AFB=∠DEC).
∴BE+EF=CF+EF,即BF=CE.
①由条件可再添加AB=DC,
在△ABF和△DCE中,
|
∴△ABF≌△DCE(SAS),
②可添加∠AFB=∠DEC,
在△ABF和△DCE中,
|
∴△ABF≌△DCE(ASA),
故答案为:AB=DC(或∠AFB=∠DEC).
点评:本题考查了全等三角形的判定.题目是开放型题目,根据已知条件结合判定方法,找出所需条件,一般答案不唯一,只要符合要求即可.

练习册系列答案
相关题目
点P(4,-3)关于原点的对称点是( )
| A、(4,3) |
| B、(-3,4) |
| C、(-4,3) |
| D、(3,-4) |
世界文化遗产长城总长约为6700000米,将6700000用科学记数法可表示为( )
| A、6.7×105 |
| B、6.7×106 |
| C、67×105 |
| D、0.67×107 |
关于y的两个一元一次方程y+3m=32与y-4=1的解相同,那么m的值为( )
| A、9 | B、-9 | C、7 | D、-8 |
下列变形正确的是( )
| A、若3x-1=2x+1,则x=0 | ||||
| B、若ac=bc,则a=b | ||||
C、若a=b,则
| ||||
D、若
|
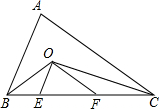 如图,△ABC中,BC=10cm,BO与CO分别为∠ABC与∠ACB的平分线,OE∥AB,OF∥AC,求△OEF的周长.
如图,△ABC中,BC=10cm,BO与CO分别为∠ABC与∠ACB的平分线,OE∥AB,OF∥AC,求△OEF的周长.