题目内容
1.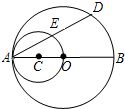 如图所示,AB是圆O的直径,以OA为直径的圆C与圆O的弦AD相交于点E.
如图所示,AB是圆O的直径,以OA为直径的圆C与圆O的弦AD相交于点E.(1)求证:点E为AD的中点.
(2)已知:BD=6cm,求弦AD的弦心距.
分析 (1)连接OE,由于OA为⊙C的直径,得到∠AEO=90°,即OE⊥AD,在⊙0中,根据垂径定理可得EA=EB;
(2)连接BD,由AB是圆O的直径,得到BD⊥AD,于是得到OE∥BD,根据三角形的中位线的性质即可得到结论.
解答 (1)证明:连接OE,
∵AO是⊙C的直径,
∴∠AEO=90°,即OE⊥AD于E,
又∵OE经过圆心O,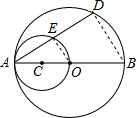
∴AE=DE,
即:点E为AD的中点;
(2)解:连接BD,
∵AB是圆O的直径,
∴BD⊥AD,
∴OE∥BD,
∵点E为AD的中点,AO=OB,
∴OE=$\frac{1}{2}$BD=3.
点评 本题考查了三角形的中位线的性质,圆周角定理的推论:直径所对的圆周角为直角;也考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
12.下列各式与x3-5x2-4x+9相等的是( )
| A. | (x3-5x2)-(-4x+9) | B. | x3-5x2-(4x+9) | C. | -(-x3+5x2)-(4x-9) | D. | x3+9-(5x2-4x) |
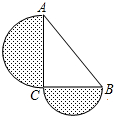 如图,在Rt△ABC中,∠C=90°,以AC、BC为直径的半圆面积分别是12.5πcm2和4.5πcm2,则Rt△ABC的面积为30cm2.
如图,在Rt△ABC中,∠C=90°,以AC、BC为直径的半圆面积分别是12.5πcm2和4.5πcm2,则Rt△ABC的面积为30cm2.