Question

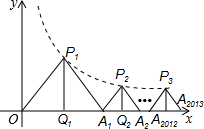如图△P₁OA₁、△P₂A₁A₂、△P₃A₂A₃、…△P₂₀₁₃A₂₀₁₂A₂₀₁₃是等腰直角三角形，点P₁、P₁、P₁、…都在函数y=

4

x

（x＞0）的图象上，斜边OA₁、A₁A₂、A₂A₃、…A₂₀₁₂A₂₀₁₃都在x轴上，则A₂₀₁₃的坐标为

 

．

Answer 1

考点：等腰直角三角形,反比例函数图象上点的坐标特征

专题：解题方法

分析：由△P₁OA₁是等腰直角三角形，P₁Q₁⊥OA₁，可得P₁Q₁=OQ₁=Q₁A₁，其它三角形都具有同样的性质，易求A₁（4，0），设P₂Q₂=a，∴OQ₂=4+a，∴P₂（4+a，a），代入y=

4

x

，得a（a+4）=4，解得a1=2

2

-2，  a2=-2

2

-2(舍去)，所以A₂的坐标为(4

2

，0)；同理可求其它各点的坐标．

解答：解：∵△P₁OA₁是等腰直角三角形，P₁Q₁⊥OA₁，
∴P₁Q₁=OQ₁=Q₁A₁，
设P₁Q₁=x，则P₁Q₁=OQ₁=Q₁A₁=x，
∴P₁（x，x），代入y=

4

x

，得x=2，
∴P₁（2，2），
∴OA₁=4，
∴A₁（4，0），
设P₂Q₂=a，
∴OQ₂=4+a，
∴P₂（4+a，a），
代入y=

4

x

，得a（a+4）=4，
解得：a1=2

2

-2，  a2=-2

2

-2(舍去)，
∴A2A1=2P2Q2=2a=2(2

2

-2)=4

2

-4，
∴OA2=OA 1+A2A 1=4+4

2

-4=4

2

，
故A₂的坐标为(4

2

，0)，
同理：可求得A3(4

3

，0)，  A4(8，0)，   A5(4

5

，0)， A6(4

6

，0) …，
故A₂₀₁₃的坐标为(4

2013

，0)．

点评：本题考查了等腰直角三角形的性质及反比例函数的性质，解题关键是探寻各个点的横坐标的规律．