题目内容
直线y=2x+1与两坐标轴围成的三角形的面积为 .
考点:一次函数图象上点的坐标特征
专题:计算题
分析:先根据坐标轴上点的坐标特征确定直线y=2x+1与坐标轴的交点坐标为(0,1)、(-
,0),然后根据三角形面积公式求解.
| 1 |
| 2 |
解答:解:当x=0时,y=2x+1=1;当y=0时,2x+1=0,解得x=-
,
所以直线y=2x+1与坐标轴的交点坐标为(0,1)、(-
,0),
所以直线y=2x+1与两坐标轴围成的三角形的面积=
×1×|-
|=
.
故答案为
.
| 1 |
| 2 |
所以直线y=2x+1与坐标轴的交点坐标为(0,1)、(-
| 1 |
| 2 |
所以直线y=2x+1与两坐标轴围成的三角形的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
故答案为
| 1 |
| 4 |
点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-bk,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
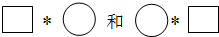 已知x、y为有理数,如果规定一种运算*,其意义是x*y=xy+1,试根据这种运算完成下列各题.
已知x、y为有理数,如果规定一种运算*,其意义是x*y=xy+1,试根据这种运算完成下列各题. 如图,某数学兴趣小组在活动课上测量学校旗杆高度,已知小红与旗杆相距12米,且小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部A的仰角为30°,求旗杆AB的高度.(参考数据:
如图,某数学兴趣小组在活动课上测量学校旗杆高度,已知小红与旗杆相距12米,且小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部A的仰角为30°,求旗杆AB的高度.(参考数据: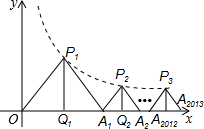 如图△P1OA1、△P2A1A2、△P3A2A3、…△P2013A2012A2013是等腰直角三角形,点P1、P1、P1、…都在函数y=
如图△P1OA1、△P2A1A2、△P3A2A3、…△P2013A2012A2013是等腰直角三角形,点P1、P1、P1、…都在函数y=