ЬтФПФкШн
ЁОЬтФПЁПЖЈвхЃКЃЈвЛЃЉШчЙћСНИіКЏЪ§y1ЃЌy2ЃЌДцдкxШЁЭЌвЛИіжЕЃЌЪЙЕУy1ЃНy2ЃЌФЧУДГЦy1ЃЌy2ЮЊЁАКЯзїКЏЪ§ЁБЃЌГЦЖдгІxЕФжЕЮЊy1ЃЌy2ЕФЁАКЯзїЕуЁБЃЛЃЈЖўЃЉШчЙћСНИіКЏЪ§ЮЊy1ЃЌy2ЮЊЁАКЯзїКЏЪ§ЁБЃЌФЧУДy1+y2ЕФзюДѓжЕГЦЮЊy1ЃЌy2ЕФЁАЙВгЎжЕЁБЃЎ
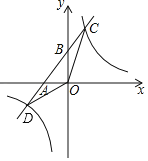
ЃЈ1ЃЉХаЖЯКЏЪ§yЃН2x+4mгыyЃН![]() ЪЧЗёЮЊЁАКЯзїКЏЪ§ЁБЃЌШчЙћЪЧЃЌЧыЧѓГіmЃН1ЪБЫќУЧЕФЁАКЯзїЕуЁБЃЛШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
ЪЧЗёЮЊЁАКЯзїКЏЪ§ЁБЃЌШчЙћЪЧЃЌЧыЧѓГіmЃН1ЪБЫќУЧЕФЁАКЯзїЕуЁБЃЛШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
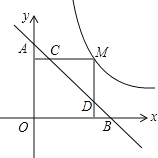
ЃЈ2ЃЉХаЖЯКЏЪ§yЃН2x+4mгыyЃНxЉ1ЃЈ|x|Ём2ЃЉЪЧЗёЮЊЁАКЯзїКЏЪ§ЁБЃЌШчЙћЪЧЃЌЧыЧѓГіЁАКЯзїЕуЁБЃЛШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
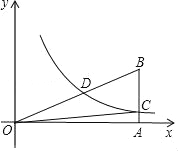
ЃЈ3ЃЉвбжЊКЏЪ§yЃНx+2mгыyЃНx2ЉЃЈ2m+1ЃЉx+ЃЈm2+4mЉ3ЃЉЃЈ0ЁмxЁм5ЃЉЪЧЁАКЯзїКЏЪ§ЁБЃЌЧвгаЮЈвЛЁАКЯзїЕуЁБЃЎ
ЂйЧѓГіmЕФШЁжЕЗЖЮЇЃЛ
ЂкШєЫќУЧЕФЁАЙВгЎжЕЁБЮЊ24ЃЌЪдЧѓГіmЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЪЧЃЌxЃНЉ3ЛђxЃН1ЃЛЃЈ2ЃЉВЛЪЧЃЌМћНтЮіЃЛЃЈ3ЃЉЂйЉ3ЁмmЃМ1Лђ2ЃМmЁм6ЃЛЂкmЃН2Љ![]() ЛђmЃН3ЃЎ
ЛђmЃН3ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩгк![]() гы
гы![]() ЖМОЙ§ЕквЛЁЂЕкШ§ЯѓЯоЃЌЫљвдСНИіКЏЪ§гаЙЋЙВЕуЃЌПЩвдХаЖЯСНИіКЏЪ§ЪЧЁАКЯзїКЏЪ§ЁБЃЌдйСЊСЂ
ЖМОЙ§ЕквЛЁЂЕкШ§ЯѓЯоЃЌЫљвдСНИіКЏЪ§гаЙЋЙВЕуЃЌПЩвдХаЖЯСНИіКЏЪ§ЪЧЁАКЯзїКЏЪ§ЁБЃЌдйСЊСЂ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() Лђ
Лђ![]() ЃЌМДПЩЧѓЁАКЯзїЕуЁБЃЛ
ЃЌМДПЩЧѓЁАКЯзїЕуЁБЃЛ
ЃЈ2ЃЉМйЩшЪЧЁАКЯзїКЏЪ§ЁБЃЌПЩЧѓЁАКЯзїЕуЁБЮЊ![]() ЃЌдйгЩ
ЃЌдйгЩ![]() ЃЌПЩЕУЕБ
ЃЌПЩЕУЕБ![]() ЪБЃЌЪЧЁАКЯзїКЏЪ§ЁБЃЛЕБ
ЪБЃЌЪЧЁАКЯзїКЏЪ§ЁБЃЛЕБ![]() Лђ
Лђ![]() ЪБЃЌВЛЪЧЁАКЯзїКЏЪ§ЁБЃЛ
ЪБЃЌВЛЪЧЁАКЯзїКЏЪ§ЁБЃЛ
ЃЈ3ЃЉЂйгЩвбжЊПЩЕУЃК![]() ЃЌНтЕУ
ЃЌНтЕУ![]() Лђ
Лђ![]() ЃЌдйгЩвбжЊПЩЕУЕБ
ЃЌдйгЩвбжЊПЩЕУЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌвђЮЊжЛгавЛИіЁАКЯзїЕуЁБдђ
ЃЌвђЮЊжЛгавЛИіЁАКЯзїЕуЁБдђ![]() Лђ
Лђ![]() ЃЛЂк
ЃЛЂк![]() ЃЌгЩЂйПЩЗжСНжжЧщПіЧѓ
ЃЌгЩЂйПЩЗжСНжжЧщПіЧѓ![]() ЕФжЕЃКЕБ
ЕФжЕЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() дк
дк![]() ЕФгазюДѓжЕЮЊ
ЕФгазюДѓжЕЮЊ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() дк
дк![]() ЕФгазюДѓжЕЮЊ
ЕФгазюДѓжЕЮЊ![]() ЃЌЗжБ№ЧѓГіЗћКЯЬѕМўЕФ
ЃЌЗжБ№ЧѓГіЗћКЯЬѕМўЕФ![]() жЕМДПЩЃЎ
жЕМДПЩЃЎ
НтЃКЃЈ1ЃЉ![]() ЪЧОЙ§ЕквЛЁЂЕкШ§ЯѓЯоЕФжБЯпЃЌ
ЪЧОЙ§ЕквЛЁЂЕкШ§ЯѓЯоЕФжБЯпЃЌ![]() ЪЧОЙ§ЕквЛЁЂЕкШ§ЯѓЯоЕФЫЋЧњЯпЃЌ
ЪЧОЙ§ЕквЛЁЂЕкШ§ЯѓЯоЕФЫЋЧњЯпЃЌ
![]() СНКЏЪ§гаЙЋЙВЕуЃЌ
СНКЏЪ§гаЙЋЙВЕуЃЌ
![]() Дцдк
Дцдк![]() ШЁЭЌвЛИіжЕЃЌЪЙЕУ
ШЁЭЌвЛИіжЕЃЌЪЙЕУ![]() ЃЌ
ЃЌ
![]() КЏЪ§
КЏЪ§![]() гы
гы![]() ЪЧЁАКЯзїКЏЪ§ЁБЃЛ
ЪЧЁАКЯзїКЏЪ§ЁБЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() Лђ
Лђ![]() ЃЌ
ЃЌ
![]() ЁАКЯзїЕуЁБЮЊ
ЁАКЯзїЕуЁБЮЊ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉМйЩшКЏЪ§![]() гы
гы![]() ЪЧЁАКЯзїКЏЪ§ЁБЃЌ
ЪЧЁАКЯзїКЏЪ§ЁБЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЕБ
ЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() гы
гы![]() ЪЧЁАКЯзїКЏЪ§ЁБЃЛЕБ
ЪЧЁАКЯзїКЏЪ§ЁБЃЛЕБ![]() Лђ
Лђ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() гы
гы![]() ВЛЪЧЁАКЯзїКЏЪ§ЁБЃЛ
ВЛЪЧЁАКЯзїКЏЪ§ЁБЃЛ
ЃЈ3ЃЉЂй![]() КЏЪ§
КЏЪ§![]() гы
гы![]() ЪЧЁАКЯзїКЏЪ§ЁБЃЌ
ЪЧЁАКЯзїКЏЪ§ЁБЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() Лђ
Лђ![]() ЃЌ
ЃЌ
![]() ЪБгаЮЈвЛКЯзїЕуЃЌ
ЪБгаЮЈвЛКЯзїЕуЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
![]() Лђ
Лђ![]() ЪБЃЌТњзуЬтвтЃЛ
ЪБЃЌТњзуЬтвтЃЛ
Ђк![]() ЃЌ
ЃЌ
![]() ЖдГЦжсЮЊ
ЖдГЦжсЮЊ![]() ЃЌ
ЃЌ
![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() дк
дк![]() ЕФгазюДѓжЕЮЊ
ЕФгазюДѓжЕЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() Лђ
Лђ![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() дк
дк![]() ЕФгазюДѓжЕЮЊ
ЕФгазюДѓжЕЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() Лђ
Лђ![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃК![]() Лђ
Лђ![]() ЃЎ
ЃЎ

ЁОЬтФПЁПдкГѕжаНзЖЮЕФКЏЪ§бЇЯАжаЃЌЮвУЧОРњСЫСаБэЁЂУшЕуЁЂСЌЯпЛКЏЪ§ЭМЯѓЃЌВЂНсКЯЭМЯѓбаОПКЏЪ§аджЪЕФЙ§ГЬЃЎвдЯТЪЧЮвУЧбаОПКЏЪ§![]() аджЪМАЦфгІгУЕФВПЗжЙ§ГЬЃЌЧыАДвЊЧѓЭъГЩЯТСаИїаЁЬтЃЎ
аджЪМАЦфгІгУЕФВПЗжЙ§ГЬЃЌЧыАДвЊЧѓЭъГЩЯТСаИїаЁЬтЃЎ
ЃЈ1ЃЉЧыАбЯТБэВЙГфЭъећЃЌВЂдкЭМжаВЙШЋИУКЏЪ§ЭМЯѓЃЛ
| Ё | Ѓ5 | Ѓ4 | Ѓ3 | Ѓ2 | Ѓ1 | 0 | 1 | 2 | 3 | 4 | 5 | Ё |
| Ё |
|
|
| Ѓ3 | 0 | 3 |
|
|
| Ё |
ЃЈ2ЃЉИљОнКЏЪ§ЭМЯѓЃЌХаЖЯЯТСаЙигкИУКЏЪ§аджЪЕФЫЕЗЈЪЧЗёе§ШЗЃЌе§ШЗЕФдкЯргІЕФРЈКХФкДђЁАЁЬЁБЃЌДэЮѓЕФдкЯргІЕФРЈКХФкДђЁАЁСЁБЃЛ
ЂйИУКЏЪ§ЭМЯѓЪЧжсЖдГЦЭМаЮЃЌЫќЕФЖдГЦжсЮЊyжсЃЛ( )
ЂкИУКЏЪ§дкздБфСПЕФШЁжЕЗЖЮЇФкЃЌгазюДѓжЕКЭзюаЁжЕЃЌЕБ![]() ЪБЃЌКЏЪ§ШЁЕУзюДѓжЕ3ЃЛЕБ
ЪБЃЌКЏЪ§ШЁЕУзюДѓжЕ3ЃЛЕБ![]() ЪБЃЌКЏЪ§ШЁЕУзюаЁжЕЃ3ЃЛ( )
ЪБЃЌКЏЪ§ШЁЕУзюаЁжЕЃ3ЃЛ( )
ЂлЕБ![]() Лђ
Лђ![]() ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЛЕБ
ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЛЕБ![]() ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЛ( )
ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЛ( )
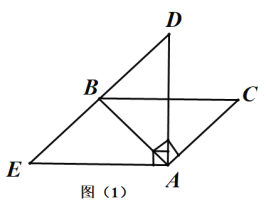
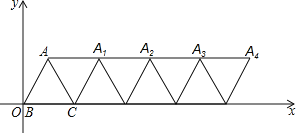
ЃЈ3ЃЉвбжЊКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃЌНсКЯФуЫљЛЕФКЏЪ§ЭМЯѓЃЌжБНгаДГіВЛЕШЪН
ЕФЭМЯѓШчЭМЫљЪОЃЌНсКЯФуЫљЛЕФКЏЪ§ЭМЯѓЃЌжБНгаДГіВЛЕШЪН![]() ЕФНтМЏЃЈБЃСє1ЮЛаЁЪ§ЃЌЮѓВюВЛГЌЙ§0.2ЃЉЃЎ
ЕФНтМЏЃЈБЃСє1ЮЛаЁЪ§ЃЌЮѓВюВЛГЌЙ§0.2ЃЉЃЎ

ЁОЬтФПЁПФГаЃзщжЏШЋаЃбЇЩњНјааСЫвЛДЮЁАЩчЛсжївхКЫаФМлжЕЙлЁБжЊЪЖОКШќЃЌШќКѓЫцЛњГщШЁСЫИїФъМЖВПЗжбЇЩњГЩМЈНјааЭГМЦЃЌжЦзїШчЯТЦЕЪ§ЗжВМБэКЭЦЕЪ§ЗжВМжБЗНЭМЃЎЧыИљОнЭМБэжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЗжЪ§ЖЮЃЈ | ЦЕЪ§ | ЦЕТЪ |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
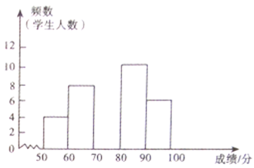
ЃЈ1ЃЉЧыЧѓГіИУаЃЫцЛњГщШЁСЫ____бЇЩњГЩМЈНјааЭГМЦЃЛ
ЃЈ2ЃЉБэжа![]() ____ЃЌ
____ЃЌ![]() ____ЃЌВЂВЙШЋжБЗНЭМЃЛ
____ЃЌВЂВЙШЋжБЗНЭМЃЛ
ЃЈ3ЃЉШєгУЩШаЮЭГМЦЭМУшЪіДЫГЩМЈЭГМЦЗжВМЧщПіЃЌдђЗжЪ§ЖЮ![]() ЖдгІЩШаЮЕФдВаФНЧЖШЪ§ЪЧ___
ЖдгІЩШаЮЕФдВаФНЧЖШЪ§ЪЧ___![]() ЃЛ
ЃЛ
ЃЈ4ЃЉШєИУаЃЙВгабЇЩњ8000ШЫЃЌЧыЙРМЦИУаЃЗжЪ§дк![]() ЕФбЇЩњгаЖрЩйШЫЃП
ЕФбЇЩњгаЖрЩйШЫЃП