题目内容
14.已知O为坐标原点,点C在x轴的正半轴上,四边形OABC是平行四边形,且∠AOC=45°,设OA=$\sqrt{2}a$,反比例函数$y=\frac{k}{x}$在第一象限内的图象经过点A,交BC于点D,D是BC边的中点.
(1)如图1,当a=4时,求k的值及边OC的长;
(2)如图2,连结AD、OD,若△OAD的面积是27,求a的值及点B的坐标.
分析 (1)先根据a=4,OA=$4\sqrt{2}$,∠AOC=45°得出A点坐标,故可得出k的值,DP⊥x轴于点P,由D是中点得出AD的长,根据等腰直角三角形的性质求出PC的长,设OC=x可得出D点坐标,代入反比例函数的解析式即可得出OC的长;
(2)根据△OAD的面积是27,点D是中点可得出平行四边形OABC面积是54,故可得出A点坐标,由A点坐标可知反比例函数是y=$\frac{{a}^{2}}{x}$,作DP⊥x轴于点P,可用a表示出D点坐标,代入反比例函数求出a的值,进而可得出结论.
解答 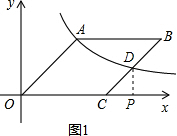 解:(1)∵a=4,OA=$4\sqrt{2}$,∠AOC=45°
解:(1)∵a=4,OA=$4\sqrt{2}$,∠AOC=45°
∴A(4,4),
∴k=16.
如图1,作DP⊥x轴于点P,
∵D是中点,
∴CD=$2\sqrt{2}$,CP=DP=2
设OC=x,则点D(x+2,2),
∵点D在反比例函数y=$\frac{16}{x}$的图象上,
∴2(x+2)=16,解得x=6,即OC=6;
(2)∵△OAD的面积是27,点D是中点,
∴平行四边形OABC面积是54.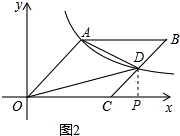
∵∠AOC=45°,OA=$\sqrt{2}$a,
∴A(a,a),
∴反比例函数是y=$\frac{{a}^{2}}{x}$,
∴54=OC×a,OC=$\frac{54}{a}$.
如图2,作DP⊥x轴于点P,
∵D是中点,PC=PD=$\frac{a}{2}$,
∴D($\frac{54}{a}$+$\frac{a}{2}$,$\frac{a}{2}$)
∵点D在图象上,
∴($\frac{54}{a}$+$\frac{a}{2}$)•$\frac{a}{2}$=a2,解得a=±6,
∴点B(15,6).
点评 本题考查的是反比例函数综合题,涉及到反比例函数图象上点的坐标特点及用待定系数法求反比例函数的解析式,根据题意作出辅助线,构造出等腰直角三角形,利用勾股定理求出D点坐标是解答此题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | x≥-$\frac{1}{2}$ | B. | x$≤-\frac{1}{2}$ | C. | x≥1 | D. | x≤1 |
| A. | -3和-1之间的有理数是-2 | |
| B. | 数轴上表示-a的点一定在原点的左边 | |
| C. | 在数轴上离开原点的距离越近的点表示的数越小 | |
| D. | -1和-2之间有无数个负数 |
