题目内容
1.以边长为a的正方形的一个顶点为圆心,以这个正六形的边长为半径画弧,得到一个扇形,再将这个扇形围成一个圆锥面,求圆锥的高.分析 设圆锥的高为h,底面圆的半径为r,由题意得,求得r=$\frac{1}{4}$a,根据勾股定理即可得到结论.
解答  解:设圆锥的高为h,底面圆的半径为r,
解:设圆锥的高为h,底面圆的半径为r,
由题意得,2πr=$\frac{90πa}{180}$,
∴r=$\frac{1}{4}$a,
∴h=$\sqrt{{a}^{2}-(\frac{1}{4}a)^{2}}$=$\frac{\sqrt{15}}{4}$a,
∴圆锥的高为$\frac{\sqrt{15}}{4}$a.
点评 本题考查了圆锥的计算,勾股定理,正确的作出图形是解题的关键.

练习册系列答案
相关题目
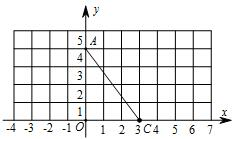 如图,在平面直角坐标系中,A(0,4),C(3,0),
如图,在平面直角坐标系中,A(0,4),C(3,0),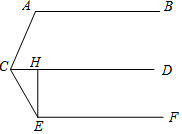 如图,已知AB∥CD∥EF,EH⊥CD,垂足为H,则∠A+∠CEH+∠ACE=270°.
如图,已知AB∥CD∥EF,EH⊥CD,垂足为H,则∠A+∠CEH+∠ACE=270°.
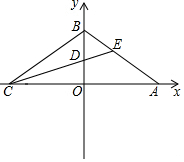 如图,直线y=-x+2与x轴交于点A,与y轴交于点B,点C在x轴上,且BC=BA,过C的直线与y轴交于点D,与线段AB交于点E.求使△OCD与△BDE面积相等时的直线CE的解析式.
如图,直线y=-x+2与x轴交于点A,与y轴交于点B,点C在x轴上,且BC=BA,过C的直线与y轴交于点D,与线段AB交于点E.求使△OCD与△BDE面积相等时的直线CE的解析式.