题目内容
20.解下列不等式(组)(1)$x-\frac{x+2}{2}≤\frac{2-x}{3}$
(2)$\left\{\begin{array}{l}2-6y≤4y+1\\ 2y-1>3({1-3y})\end{array}\right.$.
分析 (1)去分母,去括号,移项,合并同类项,系数化成1即可;
(2)求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:(1)去分母得:6x-3(x+2)≤2(2-x),
6x-3x-6≤4-2x,
6x-3x+2x≤4+6,
5x≤10,
x≤2;
(2)$\left\{\begin{array}{l}{2-6y≤4y+1①}\\{2y-1>3(1-3y)②}\end{array}\right.$
∵解不等式①得:y≥$\frac{1}{10}$,
解不等式②得:y>$\frac{4}{11}$,
∴不等式组的解集为$y>\frac{4}{11}$.
点评 本题考查了解一元一次不等式和解一元一次不等式组的应用,能正确根据不等式的基本性质求出不等式的解集是解此题的关键.

练习册系列答案
相关题目
12. 如图,一根木棒AB的长为2m斜靠在与地面垂直的墙上,与地面的倾斜角∠ABO为60°,当木棒沿墙壁向下滑动至A′,AA′=$\sqrt{3}-\sqrt{2}$,B端沿地面向右滑动至点B′,则木棒中点从P随之运动至P′所经过的路径长为( )
如图,一根木棒AB的长为2m斜靠在与地面垂直的墙上,与地面的倾斜角∠ABO为60°,当木棒沿墙壁向下滑动至A′,AA′=$\sqrt{3}-\sqrt{2}$,B端沿地面向右滑动至点B′,则木棒中点从P随之运动至P′所经过的路径长为( )
 如图,一根木棒AB的长为2m斜靠在与地面垂直的墙上,与地面的倾斜角∠ABO为60°,当木棒沿墙壁向下滑动至A′,AA′=$\sqrt{3}-\sqrt{2}$,B端沿地面向右滑动至点B′,则木棒中点从P随之运动至P′所经过的路径长为( )
如图,一根木棒AB的长为2m斜靠在与地面垂直的墙上,与地面的倾斜角∠ABO为60°,当木棒沿墙壁向下滑动至A′,AA′=$\sqrt{3}-\sqrt{2}$,B端沿地面向右滑动至点B′,则木棒中点从P随之运动至P′所经过的路径长为( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
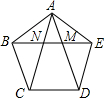 如图,在正五边形ABCDE中,对角线AD、AC与EB分别交于点M、N.
如图,在正五边形ABCDE中,对角线AD、AC与EB分别交于点M、N.



 如图,在菱形ABCD中,O为对角线AC与BD的交点,M、N分别是OA、OC的中点.
如图,在菱形ABCD中,O为对角线AC与BD的交点,M、N分别是OA、OC的中点.