Question

12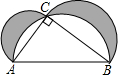．如图，阴影部分表示以直角三角形各边为直径的三个半圆所围成的两个新月形，它的面积与直角三角形的面积有什么关系？请说明理由．

Answer 1

分析 用AC，BC及AB表示出阴影部分的面积，再与三角形的面积公式相比较即可．

解答 解：相等．
理由：∵AC²+BC²=AB²，
∴S_阴影=$\frac{1}{2}$π（$\frac{AC}{2}$）²+$\frac{1}{2}$π（$\frac{BC}{2}$）²+$\frac{1}{2}$AC×BC-$\frac{1}{2}$π（$\frac{AB}{2}$）²，
=$\frac{1}{2}$π[$\frac{1}{4}$AC²+$\frac{1}{4}$BC²-$\frac{1}{4}$AB²]+$\frac{1}{2}$AC×BC，
=$\frac{1}{2}$AC×BC，
∴它的面积与直角三角形的面积相等．

点评 本题考查了勾股定理．解题的关键是找出阴影部分面积的表达式．