Question

8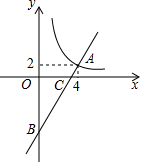．如图，一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A（4，2），与y轴的负半轴交于点B，且OB=6，
（1）求函数y=$\frac{m}{x}$和y=kx+b的解析式．
（2）已知直线AB与x轴相交于点C，在第一象限内，求反比例函数y=$\frac{m}{x}$的图象上一点P，使得S_△POC=9．

Answer 1

分析 （1）把点A（4，2）代入反比例函数y=$\frac{m}{x}$，可得反比例函数解析式，把点A（4，2），B（0，-6）代入一次函数y=kx+b，可得一次函数解析式；
（2）根据C（3，0），可得CO=3，设P（a，$\frac{8}{a}$），根据S_△POC=9，可得$\frac{1}{2}$×3×$\frac{8}{a}$=9，解得a=$\frac{4}{3}$，即可得到点P的坐标．

解答 解：（1）把点A（4，2）代入反比例函数y=$\frac{m}{x}$，可得m=8，
∴反比例函数解析式为y=$\frac{8}{x}$，
∵OB=6，
∴B（0，-6），
把点A（4，2），B（0，-6）代入一次函数y=kx+b，可得
$\left\{\begin{array}{l}{2=4k+b}\\{-6=b}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=2}\\{b=-6}\end{array}\right.$，
∴一次函数解析式为y=2x-6；

（2）在y=2x-6中，令y=0，则x=3，
即C（3，0），
∴CO=3，
设P（a，$\frac{8}{a}$），则
由S_△POC=9，可得$\frac{1}{2}$×3×$\frac{8}{a}$=9，
解得a=$\frac{4}{3}$，
∴P（$\frac{4}{3}$，6）．

点评 本题主要考查了反比例函数与一次函数交点问题，解题时注意：反比例函数与一次函数交点坐标同时满足两个函数解析式．