题目内容
已知矩形ABCD边长为AB为2,AD=3,B(3,0),D(1,3),有一点P(O,m)在x轴上移动,-6<m<0,问过P、A、B三点且对称轴平行于y轴的抛物线顶点是否在此矩形ABCD内部?
考点:二次函数的性质
专题:
分析:根据矩形的性质求出点A的坐标,然后设抛物线解析式为y=a(x-1)(x-3),然后把点P的坐标代入求出a,再求出顶点的纵坐标,然后根据m的取值范围求解即可.
解答: 解:∵D(1,3),
解:∵D(1,3),
∴A(1,0),
设抛物线解析式为y=a(x-1)(x-3),
把点P(0,m)代入得,3a=m,
所以,a=
,
∴y=
(x-2)2-
,
∵-6<m<0,
∴0<-
<2,
∵AD=3,对称轴为直线x=2,
∴抛物线的顶点此矩形ABCD内部.
 解:∵D(1,3),
解:∵D(1,3),∴A(1,0),
设抛物线解析式为y=a(x-1)(x-3),
把点P(0,m)代入得,3a=m,
所以,a=
| m |
| 3 |
∴y=
| m |
| 3 |
| m |
| 3 |
∵-6<m<0,
∴0<-
| m |
| 3 |
∵AD=3,对称轴为直线x=2,
∴抛物线的顶点此矩形ABCD内部.
点评:本题考查了二次函数的性质,矩形的性质,确定出点A的坐标,然后用m表示出抛物线解析式是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
如果x:y=2:3,则下列各式不成立的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图是一个长方形的表面展开图,每个面上都标有一个数字,将它折叠复原成长方形,并使写有数字的面朝外.
如图是一个长方形的表面展开图,每个面上都标有一个数字,将它折叠复原成长方形,并使写有数字的面朝外.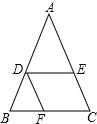 如图所示,已知DE∥BC,DF∥AC,且AE=3,AC=5,BC=10,求BF的长.
如图所示,已知DE∥BC,DF∥AC,且AE=3,AC=5,BC=10,求BF的长.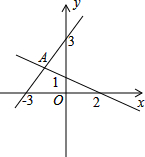 如图,直线l1与l2相交于点A,求A点的坐标.
如图,直线l1与l2相交于点A,求A点的坐标. 如图,在一建筑物上悬挂有一个长20m的条幅AB,某人从住宅楼的阳台C处观测条幅顶端A点的仰角为45°,测得条幅底端B点的俯角为30°,求建筑物和住宅楼的水平距离DE.(保留到十分位,
如图,在一建筑物上悬挂有一个长20m的条幅AB,某人从住宅楼的阳台C处观测条幅顶端A点的仰角为45°,测得条幅底端B点的俯角为30°,求建筑物和住宅楼的水平距离DE.(保留到十分位,