题目内容
如图:B、C是x轴上两点,以BC为直径的圆交y轴的正半轴于点A,点B、C的坐标分别是(-12,0),(4,0)(1)求点A的坐标.
(2)一动点P以每秒1个单位长度的速度从点C开始沿CB运动到B停止.过点P作PD⊥AC于D,设点P的运动时间为t.求t为何值时,△PAD与△ABC相似?
(3)在x轴上是否存在点M使△ABM是等腰三角形?若存在,直接写出所有满足条件的点M的坐标;若不存在,请说明理由.

【答案】分析:(1)取线段BC的中点E,连接AE.在直角△AEO中,根据勾股定理即可求得线段OA的长度;
(2)需要分类讨论:①△PAD∽△BCA;②△PAD∽△CBA;
(3)需要分类讨论:①以AB为底的等腰三角形;②以AM为底的等腰三角形.
解答: 解:(1)如图1,取线段BC的中点E,连接AE.
解:(1)如图1,取线段BC的中点E,连接AE.
∵点B、C的坐标分别是(-12,0),(4,0),
∴BC=16.
又∵BC是直径,
∴点E是圆心,且BE=CE=AE=8,OE=4.
∴在Rt△AEO中,根据勾股定理知OA= =
= =4
=4 ,
,
∴点A的坐标是(0,4 );
);
(2)易求AB=8 ,AC=8.
,AC=8.
∵BC是直径,
∴BA⊥AC.
又∵PD⊥AC,
∴PD∥AB,
∴ =
= ,即
,即 =
= ,则PD=
,则PD= .
.
 =
= ,则
,则 =
= ,即
,即 =
= ,则AD=8-
,则AD=8- .
.
∵∠PDA=∠BAC=90°,
∴△PAD与△ABC相似分两种情况:
①当①△PAD∽△BCA时, =
= ,即
,即 =
= ,
,
解得,t=24+8 (不合题意,舍去),或t=24-8
(不合题意,舍去),或t=24-8 ;
;
②当△PAD∽△CBA时, =
= ,即
,即 =
= ,
,
解得,t=40+8 (不合题意,舍去),或t=40-8
(不合题意,舍去),或t=40-8 .
.
综上所述,t=24-8 或t=40-8
或t=40-8 .
.
(3)如图3,当AB=BM时,点M的坐标是M1(8 -12,0)、
-12,0)、
M3(-8 -12,0);
-12,0);
当AB=BM时,点M的坐标是M2(-4,0);
综上所述,符合条件的点M的坐标是M1(8 -12,0)、M3(-8
-12,0)、M3(-8 -12,0)、M2(-4,0).
-12,0)、M2(-4,0).
点评:本题考查了圆的综合题.其中涉及到的知识点有圆周角定理、相似三角形的判定与性质、等腰三角形的判定以及平行线截线段成比例等知识点.解题时,注意分类讨论,以防漏解.
(2)需要分类讨论:①△PAD∽△BCA;②△PAD∽△CBA;
(3)需要分类讨论:①以AB为底的等腰三角形;②以AM为底的等腰三角形.
解答:
 解:(1)如图1,取线段BC的中点E,连接AE.
解:(1)如图1,取线段BC的中点E,连接AE.∵点B、C的坐标分别是(-12,0),(4,0),
∴BC=16.
又∵BC是直径,
∴点E是圆心,且BE=CE=AE=8,OE=4.
∴在Rt△AEO中,根据勾股定理知OA=
 =
= =4
=4 ,
,∴点A的坐标是(0,4
 );
);(2)易求AB=8
 ,AC=8.
,AC=8.
∵BC是直径,
∴BA⊥AC.
又∵PD⊥AC,
∴PD∥AB,
∴
 =
= ,即
,即 =
= ,则PD=
,则PD= .
. =
= ,则
,则 =
= ,即
,即 =
= ,则AD=8-
,则AD=8- .
.∵∠PDA=∠BAC=90°,
∴△PAD与△ABC相似分两种情况:
①当①△PAD∽△BCA时,
 =
= ,即
,即 =
= ,
,解得,t=24+8
 (不合题意,舍去),或t=24-8
(不合题意,舍去),或t=24-8 ;
;
②当△PAD∽△CBA时,
 =
= ,即
,即 =
= ,
,解得,t=40+8
 (不合题意,舍去),或t=40-8
(不合题意,舍去),或t=40-8 .
.综上所述,t=24-8
 或t=40-8
或t=40-8 .
.(3)如图3,当AB=BM时,点M的坐标是M1(8
 -12,0)、
-12,0)、M3(-8
 -12,0);
-12,0);当AB=BM时,点M的坐标是M2(-4,0);
综上所述,符合条件的点M的坐标是M1(8
 -12,0)、M3(-8
-12,0)、M3(-8 -12,0)、M2(-4,0).
-12,0)、M2(-4,0).点评:本题考查了圆的综合题.其中涉及到的知识点有圆周角定理、相似三角形的判定与性质、等腰三角形的判定以及平行线截线段成比例等知识点.解题时,注意分类讨论,以防漏解.

练习册系列答案
相关题目
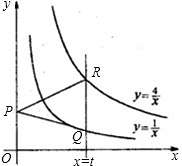 个函数图象分别交于点Q、R,连接PQ、PR.
个函数图象分别交于点Q、R,连接PQ、PR. 点P的坐标;若不存在,请说明理由.
点P的坐标;若不存在,请说明理由. 如图:B、C是x轴上两点,以BC为直径的圆交y轴的正半轴于点A,点B、C的坐标分别是(-12,0),(4,0)
如图:B、C是x轴上两点,以BC为直径的圆交y轴的正半轴于点A,点B、C的坐标分别是(-12,0),(4,0)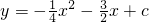 与x轴交于A、B两点(A在B的左边),与y轴交于点C,OC=4.
与x轴交于A、B两点(A在B的左边),与y轴交于点C,OC=4. 点P的坐标;若不存在,请说明理由.
点P的坐标;若不存在,请说明理由. 与x轴交于A、B两点(A在B的左边),与y轴交于点C,OC=4.
与x轴交于A、B两点(A在B的左边),与y轴交于点C,OC=4.