Question

如图，抛物线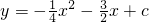与x轴交于A、B两点（A在B的左边），与y轴交于点C，OC=4．
（1）直接填空：c=______；
（2）点Q是抛物线上一点，且横坐标为-4．
①若线段BQ的中点为M，如图1，连接CM，求证：CM⊥BQ；
②如图2，点P是y轴上一个动点，是否存在这样的点P，使得△BPQ是直角三角形？如果存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

解：（1）∵OC=4．
∴C（0，4），且C点在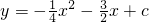上，
∴c=4
故答案为：4

（2）①连接CQ、BC．
由（1）得：c=4，则抛物线的解析式是．
∵点Q在抛物线上，且横坐标为-4，
∴当x=-4时，y=6，
∴点Q坐标为（-4，6）．
连接QC、BC，作QT⊥y轴于点T，如图．
令y=0，则，解得：x₁=2或x₂=-8，则OB=2
在Rt△BOC中，由勾股定理得：BC²=OB²+OC²=2²+4²=20
在Rt△QTC中，由勾股定理得：QC²=QT²+CT²=4²+（6-4）²=20
∴BC=QC，即△BCQ是等腰三角形．
又点M为线段BQ的中点，
∴CM⊥BQ．
②存在．理由如下：
设P的坐标为（0，n），在△BPQ中，
若∠BQP=90°，由勾股定理得：PQ²+BQ²=BP²，
∴4²+（n-6）²+6²+（2+4）²=2²+n²，解得n=10，
此时点P的坐标为P₁（0，10）．…
若∠QBP=90°，由勾股定理得：PQ²=BQ²+BP²，
∴4²+（6-n）²=6²+（2+4）²+2²+n²，解得n=-2，
此时点P的坐标为P₂（0，-2）．…
若∠QPB=90°，由勾股定理得：BQ²=BP²+PQ²
∴6²+（2+4）²=4²+（n-6）²+2²+n²，解得，
∴点P的坐标为或．
综上，存在这样的点P，使得△BPQ是直角三角形，点P的坐标为：
（0，10）、（0，-2）、或．
分析：（1）由条件根据抛物线的解析式可以求出C点的坐标，然后再代入抛物线的解析式就可以求出c值．
（2）①根据已知条件可以求出Q点的坐标，再连接CQ、BC，利用勾股定理求出BC、QC的长，从而证明△QBC为等腰三角形，根据等腰三角形的性质可以证明结论．
②使得△BPQ是直角三角形分三种情况：当∠BQP=90°、∠QBP=90°、∠QPB=90°时，设出点P的坐标，利用勾股定理就可以求出结论．
点评：本题是一道二次函数的综合试题，考查了二次函数的性质，待定系数法求一次函数的解析式，等腰三角形的性质，直角三角形的性质，勾股定理的运用．