Question

函数y=

1

x

、y=

4

x

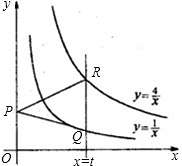（x＞0）的图象如图所示．P是y轴上的任意一点，直线x=t（t＞0）与两个函数图象分别交于点Q、R，连接PQ、PR．
（1）当t=3时，求△PQR的面积；
（2）当t从小到大变化时，△PQR的面积是否发生变化，说明理由．

Answer 1

分析：（1）△PQR的面积=QR×t÷2；
（2）用t表示出△PQR的面积，看是否为一个定值．

解答：解：（1）∵直线x=t（t＞0）与两个函数图象分别交于点Q、R，
∴当t=3时，y_Q=

1

x

=

1

3

，y_R=

4

x

=

4

3

，
∴QR=|y_R-y_Q|=1，
∴s_△PQR=

1

2

×1×3=

3

2

；

（2）当x=t时，Q的纵坐标为

1

t

，R的纵坐标为

4

t

，
∴QR=

3

t

，
∴s_△PQR=

1

2

×t×

3

t

=

3

2

为一个定值，没变化．

点评：解决本题的关键是正确得到所求三角形的面积的关系式．利用形数结合解决此类问题，是非常有效的方法．