题目内容
抛物线y=（x-2）2+1的顶点坐标是（ ）
| A、（2，1） |
| B、（-2，-1） |
| C、（-2，1） |
| D、（2，-1） |
考点：二次函数的性质
专题：
分析：已知抛物线的顶点式，可知顶点坐标和对称轴．
解答：解：∵y=（x-2）2+1是抛物线的顶点式，
根据顶点式的坐标特点可知，
对称轴为直线x=2，
故选A．
根据顶点式的坐标特点可知，
对称轴为直线x=2，
故选A．
点评：考查了二次函数的性质，顶点式y=a（x-h）2+k，顶点坐标是（h，k），对称轴是x=h．
练习册系列答案
相关题目
a、b为任何非零有理数，则
+
+
的可能取值是（ ）
| a |
| |a| |
| b |
| |b| |
| ab |
| |ab| |
| A、-3或1 | B、3或1或-1 |
| C、1或3 | D、-1或3 |
下列结论正确的是（ ）
| A、有两个锐角相等的两个直角三角形全等 |
| B、一条斜边对应相等的两个直角三角形全等 |
| C、两个等边三角形全等 |
| D、顶角和底边对应相等的两个等腰三角形全等 |
如图，在六边形的顶点处，分别标上数1、2、3、4、5、6，能否使任意三个相邻顶点处的三个数之和大于9？若能，请在图中标出来；若不能，请说明理由．
如图，已知AC=DB，要使△△ABC≌△DCB，只需增加的一个条件是（ ）| A、∠A=∠D |
| B、∠ABD=∠DCA |
| C、∠ACB=∠DBC |
| D、∠ABC=∠DCB |
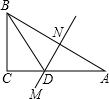如图，在△ABC中，∠C=90°，AC=24cm，AB的垂直平分线MN交AC于D，连接BD，若cos∠BDC=| 3 |
| 5 |
| A、12cm | B、9cm |
| C、24cm | D、14cm |
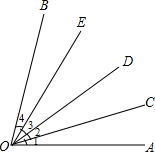如图，∠1=∠2=∠3=∠4，根据图形回答：