题目内容
下列结论正确的是( )
| A、有两个锐角相等的两个直角三角形全等 |
| B、一条斜边对应相等的两个直角三角形全等 |
| C、两个等边三角形全等 |
| D、顶角和底边对应相等的两个等腰三角形全等 |
考点:全等三角形的判定
专题:
分析:利用三角形全等的判定方法逐项判断即可.
解答:解:A、当有两个锐角相等的直角三角形中,满足AAA,不能全等,故A不正确;
B、斜边对应相等,但是直角边不一定相等,所以不能证明全等,故B不正确;
C、等边三角形如果边不相等也不一定全等,所以C不正确;
D、顶角对应相等,由等腰三角形的性质可知底角也相等,加上底边对应相等,所以可以利用ASA或AAS判定全等,所以D正确;
故选D.
B、斜边对应相等,但是直角边不一定相等,所以不能证明全等,故B不正确;
C、等边三角形如果边不相等也不一定全等,所以C不正确;
D、顶角对应相等,由等腰三角形的性质可知底角也相等,加上底边对应相等,所以可以利用ASA或AAS判定全等,所以D正确;
故选D.
点评:本题主要考查全等三角形的判定,掌握三角形全等的判定方法是解题的关键,注意AAA和ASS不能判定两个三角形全等.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
下列等式正确的是( )
| A、(2x)3=2x3 |
| B、a2•a3=a6 |
| C、π6÷π3=π2 |
| D、x9÷x5=x4 |
若一次函数y=kx+b的图象交x轴于(2,0),交y轴于(0,3),则不等式kx+b>0的解集是( )
| A、x>2 | B、x<2 |
| C、x>3 | D、x<3 |
下列计算结果相等的为( )
| A、23和32 | ||||
B、-23和
| ||||
| C、-32和(-3)2 | ||||
| D、(-1)2 和(-1)2n-2(n是大小1的整数) |
若x1,x2是方程x2-6x+8的两根,则x1+x2的值是( )
| A、8 | B、-8 | C、-6 | D、6 |
抛物线y=(x-2)2+1的顶点坐标是( )
| A、(2,1) |
| B、(-2,-1) |
| C、(-2,1) |
| D、(2,-1) |
在同学们学习的运算法则中,我们补充定义新运算“%”,它的运算规则是:a%b=(a-b)×(b-a),则3%6=( )
| A、9 | B、18 | C、-9 | D、2 |
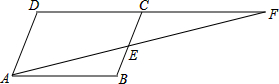 如图,?ABCD中,E为BC中点,连接AE交DC的延长线于F,求证:AE=EF.
如图,?ABCD中,E为BC中点,连接AE交DC的延长线于F,求证:AE=EF.