题目内容
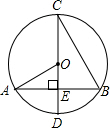如图，CD是⊙O的直径，弦AB交CD于点E，CE=AB=8，∠AOD=2∠BCD，则⊙O的直径为（ ）| A、5 | ||
| B、8 | ||
| C、10 | ||
D、8
|
考点：垂径定理,勾股定理,圆周角定理
专题：
分析：先根据∠AOD=2∠BCD得出
=
，故CD⊥AB，所以可得出AE的长，设OA=r，则OE=8-r，根据勾股定理求出r的值即可．
 |
| AD |
|
| BD |
解答：解：∵∠AOD=2∠BCD，
∴
=
，
∴CD⊥AB，
∵CE=AB=8，
∴AE=4．
设OA=r，则OE=8-r，
在Rt△AOE中，OE2+AE2=OA2，即（8-r）2+42=r2，解得r=5．
∴⊙O的直径=2r=10．
故选C．
∴
|
| AD |
|
| BD |
∴CD⊥AB，
∵CE=AB=8，
∴AE=4．
设OA=r，则OE=8-r，
在Rt△AOE中，OE2+AE2=OA2，即（8-r）2+42=r2，解得r=5．
∴⊙O的直径=2r=10．
故选C．
点评：本题考查的是垂径定理，熟知平分弦的直径平分这条弦，并且平分弦所对的两条弧是解答此题的关键．
练习册系列答案
学业测评一课一测系列答案
小学课时作业全通练案系列答案
相关题目
已知一次函数y=kx+b，当0≤x≤2时，对应的函数值y的取值范围是-2≤y≤4，则k的值为（ ）
| A、3 | B、-3 |
| C、3或-3 | D、k的值不确定 |
已知△ABC≌△DEF，且△ABC的周长为15，若AC=4，EF=6，则AB=（ ）
| A、4 | B、5 | C、6 | D、5或6 |
如图，点B1是边长为1的等边△OBA的两条中线的交点，以OB1为一边，构造等边△OB1A1（点O，B1，A1按逆时针方向排列），称为第一次构造；点B2是△OB1A1的两条中线的交点，再以OB2为一边．构造等边△OB2A2（点O，B2，A2按逆时针方向排列），称为第二次构造；以此类推，…
如图，⊙O的半径为2，直径CD经过弦AB的中点G，∠ADC=75°．