题目内容
 如图,点B1是边长为1的等边△OBA的两条中线的交点,以OB1为一边,构造等边△OB1A1(点O,B1,A1按逆时针方向排列),称为第一次构造;点B2是△OB1A1的两条中线的交点,再以OB2为一边.构造等边△OB2A2(点O,B2,A2按逆时针方向排列),称为第二次构造;以此类推,…
如图,点B1是边长为1的等边△OBA的两条中线的交点,以OB1为一边,构造等边△OB1A1(点O,B1,A1按逆时针方向排列),称为第一次构造;点B2是△OB1A1的两条中线的交点,再以OB2为一边.构造等边△OB2A2(点O,B2,A2按逆时针方向排列),称为第二次构造;以此类推,…(1)求OB1的长;
(2)直接写S△OA1B1及S△OA2B2的值(不要求写过程);
(3)当第n次构造出的等边△OBnAn的边OAn与等边△OBA的边OB第一次重合时,构造停止,则构造出的最后一个三角形的面积是
考点:等边三角形的性质
专题:规律型
分析:(1)根据题意求出OC=
OA=
,即可得出OB1=
=
;
(2)根据等边三角形的面积求出S△OA1B1=
;再求出OB2=
,即可求出S△OA2B2=
OB22;
(3)由(1)(2)得出规律,得出S△OA10B10=(
)10S△ABC.
| 1 |
| 2 |
| 1 |
| 2 |
| OC |
| cos30° |
| ||
| 3 |
(2)根据等边三角形的面积求出S△OA1B1=
| ||
| 12 |
| 1 |
| 3 |
| ||
| 4 |
(3)由(1)(2)得出规律,得出S△OA10B10=(
| 1 |
| 3 |
解答:解:(1)∵B1是边长为1的等边△OBA的两条中线的交点,
∴点B1是△OBA的重心,也是内心,也是外心,
∴∠B1OB2=30°,OC=
OA=
,
∴OB1=
=
=
;
(2)S△OA1B1=
OB12=
;
∵OB2=
=
,
∴S△OA2B2=
OB22=
×
=
;
(3)∵点B1是边长为1的等边△OBA的两条中线的交点,
∴点B1是△OBA的重心,也是内心,
∴∠BOB1=30°,
∵△OB1A1是等边三角形,
∴∠A1OB=60°+30°=90°,
∵每构造一次三角形,OBi 边与OB边的夹角增加30°,
∴还需要(360-90)÷30=9,即一共1+9=10次构造后等边△OBnAn的边OAn与等边△OBA的边OB第一次重合,
∴构造出的最后一个三角形为等边△OB10A10,
∵S△OA1B1=
S△ABC,S△OA2B2=
S△OA1B1=(
)2S△ABC,…,
∴S△OA10B10=(
)10S△ABC=
;
故答案为:
.
∴点B1是△OBA的重心,也是内心,也是外心,
∴∠B1OB2=30°,OC=
| 1 |
| 2 |
| 1 |
| 2 |
∴OB1=
| OC |
| cos30° |
| ||||
|
| ||
| 3 |
(2)S△OA1B1=
| ||
| 4 |
| ||
| 12 |
∵OB2=
| ||
| cos30° |
| 1 |
| 3 |
∴S△OA2B2=
| ||
| 4 |
| ||
| 4 |
| 1 |
| 9 |
| ||
| 36 |
(3)∵点B1是边长为1的等边△OBA的两条中线的交点,
∴点B1是△OBA的重心,也是内心,
∴∠BOB1=30°,
∵△OB1A1是等边三角形,
∴∠A1OB=60°+30°=90°,
∵每构造一次三角形,OBi 边与OB边的夹角增加30°,
∴还需要(360-90)÷30=9,即一共1+9=10次构造后等边△OBnAn的边OAn与等边△OBA的边OB第一次重合,
∴构造出的最后一个三角形为等边△OB10A10,
∵S△OA1B1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴S△OA10B10=(
| 1 |
| 3 |
| ||
| 4×310 |
故答案为:
| ||
| 4×310 |
点评:本题考查了等边三角形的性质,三角函数的定义,相似三角形的判定与性质等知识,有一定难度.特别是第(3)问中,根据条件判断构造出的最后一个三角形为等边△OB10A10及利用相似三角形的面积比等于相似比的平方,得出△OB1A1与△OBA的面积比为
,进而总结出规律是解题的关键.
| 1 |
| 3 |

练习册系列答案
相关题目
计算(2x-3y)(4x2+6xy+9y2)的正确结果是( )
| A、(2x-3y)2 |
| B、(2x+3y)2 |
| C、8x3-27y3 |
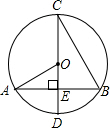 如图,CD是⊙O的直径,弦AB交CD于点E,CE=AB=8,∠AOD=2∠BCD,则⊙O的直径为( )
如图,CD是⊙O的直径,弦AB交CD于点E,CE=AB=8,∠AOD=2∠BCD,则⊙O的直径为( )| A、5 | ||
| B、8 | ||
| C、10 | ||
D、8
|
甲队有32人,乙队有28人,现从乙队抽x人到甲队,使甲队人数是乙队人数的2倍,据题意可列方程为( )
| A、32+x=56 |
| B、32=2(28-x) |
| C、32+x=2(28-x) |
| D、2(32+x)=28-x |