题目内容
 如图,⊙O的半径为2,直径CD经过弦AB的中点G,∠ADC=75°.
如图,⊙O的半径为2,直径CD经过弦AB的中点G,∠ADC=75°.(1)填空:cos∠ACB=
(2)求OG的长.
考点:垂径定理,勾股定理,圆周角定理,特殊角的三角函数值
专题:
分析:(1)先根据圆周角定理得出∠ABC=∠ADC=75°,再由垂径定理得出
=
,故
=
,由此可得出∠BAC的度数,由三角形内角和定理可得出结论;
(2)连接OA,根据直角三角形的性质求出∠ACG的度数,由圆周角定理求出∠AOG的度数,根据直角三角形的性质可得出结论.
 |
| AD |
 |
| BD |
 |
| AC |
 |
| BC |
(2)连接OA,根据直角三角形的性质求出∠ACG的度数,由圆周角定理求出∠AOG的度数,根据直角三角形的性质可得出结论.
解答: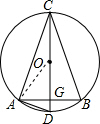 解:(1)∵∠ADC=75°,
解:(1)∵∠ADC=75°,
∴∠ABC=∠ADC=75°.
∵直径CD经过弦AB的中点G,
∴
=
,
∴
=
,
∴∠BAC=∠ABC=75°,
∴∠ACB=180°-75°-75°=30°,
∴cos∠ACB=cos30°=
.
故答案为:
;
(2)连接OA,
∵直径CD经过弦AB的中点G,
∴AB⊥CD.
∵∠BAC=75°,
∴∠ACG=90°-75°=15°,
∴∠AOG=30°.
∵OA=2,
∴OG=OA•cos30°=2×
=
.
 解:(1)∵∠ADC=75°,
解:(1)∵∠ADC=75°,∴∠ABC=∠ADC=75°.
∵直径CD经过弦AB的中点G,
∴
 |
| AD |
 |
| BD |
∴
 |
| AC |
 |
| BC |
∴∠BAC=∠ABC=75°,
∴∠ACB=180°-75°-75°=30°,
∴cos∠ACB=cos30°=
| ||
| 2 |
故答案为:
| ||
| 2 |
(2)连接OA,
∵直径CD经过弦AB的中点G,
∴AB⊥CD.
∵∠BAC=75°,
∴∠ACG=90°-75°=15°,
∴∠AOG=30°.
∵OA=2,
∴OG=OA•cos30°=2×
| ||
| 2 |
| 3 |
点评:本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
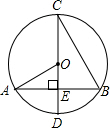 如图,CD是⊙O的直径,弦AB交CD于点E,CE=AB=8,∠AOD=2∠BCD,则⊙O的直径为( )
如图,CD是⊙O的直径,弦AB交CD于点E,CE=AB=8,∠AOD=2∠BCD,则⊙O的直径为( )| A、5 | ||
| B、8 | ||
| C、10 | ||
D、8
|
 下面图表是交警在一个路口统计的某个时段来往车辆的车速情况,则这些车辆的平均速度为
下面图表是交警在一个路口统计的某个时段来往车辆的车速情况,则这些车辆的平均速度为