题目内容
 如图,在正方形ABCD中,OE=OF.求证:
如图,在正方形ABCD中,OE=OF.求证:(1)AE=BF;
(2)AE⊥BF.
考点:全等三角形的判定与性质,正方形的性质
专题:证明题
分析:(1)如图,证明△AOE≌△BOF,得到AE=BF,即可解决问题.
(2)如图,作辅助线;证明∠AEO=∠AFG.证明∠GAF+∠AFG=90°,即可解决问题.
(2)如图,作辅助线;证明∠AEO=∠AFG.证明∠GAF+∠AFG=90°,即可解决问题.
解答: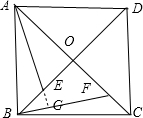 证明:(1)如图,
证明:(1)如图,
∵四边形ABCD为正方形,
∴OA=OB,∠AOE=∠BOF;
在△AOE与△BOF中,
,
∴△AOE≌△BOF(SAS),
∴AE=BF.
(2)如图,延长AE交BF于点G;
∵△AOE≌△BOF,
∴∠AEO=∠OFG,即∠AEO=∠AFG.
∵AO⊥EO,
∴∠EAO+∠AEO=90°,
∴∠GAF+∠AFG=90°,
∴AE⊥BF.
 证明:(1)如图,
证明:(1)如图,∵四边形ABCD为正方形,
∴OA=OB,∠AOE=∠BOF;
在△AOE与△BOF中,
|
∴△AOE≌△BOF(SAS),
∴AE=BF.
(2)如图,延长AE交BF于点G;
∵△AOE≌△BOF,
∴∠AEO=∠OFG,即∠AEO=∠AFG.
∵AO⊥EO,
∴∠EAO+∠AEO=90°,
∴∠GAF+∠AFG=90°,
∴AE⊥BF.
点评:该题主要考查了正方形的性质、全等三角形的判定及其性质等几何知识点及其应用问题;解题的关键是抓住图形中隐含的数量关系,数形结合,灵活运用正方形的性质、全等三角形的判定等来分析、判断、解答.

练习册系列答案
相关题目
如图,下列选项中不是正六棱柱三视图的是( )
A、 |
B、 |
C、 |
D、 |
 如图,∠MBN=60°,在∠MBN的内部有一点C,且BC=10,点D、E分别在BM、BN上,则△CDE周长的最小值为
如图,∠MBN=60°,在∠MBN的内部有一点C,且BC=10,点D、E分别在BM、BN上,则△CDE周长的最小值为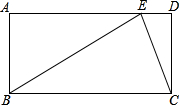 如图,矩形ABCD中,E是AD上一点,BC=BE=2CD,求∠DCE的度数.
如图,矩形ABCD中,E是AD上一点,BC=BE=2CD,求∠DCE的度数. △BCD中,BC=CD,∠BCD=90°,E是△BCD外一点,CE∥BD,且BE=BD,求
△BCD中,BC=CD,∠BCD=90°,E是△BCD外一点,CE∥BD,且BE=BD,求