题目内容
 如图,∠MBN=60°,在∠MBN的内部有一点C,且BC=10,点D、E分别在BM、BN上,则△CDE周长的最小值为
如图,∠MBN=60°,在∠MBN的内部有一点C,且BC=10,点D、E分别在BM、BN上,则△CDE周长的最小值为考点:轴对称-最短路线问题
专题:
分析:设点C关于BM的对称点为C′,关于BN的对称点为C″,当点D、E在C′C″上时,△CDE的周长最小.根据轴对称的性质得出DC=DC′,BC=BC′,∠C′BM=∠CBM;EC=EC″,BC=BC″,∠NBC″=∠NBC,从而得出BC′=BC″=OC=10,∠C′BC″=120°,得出△C′BC″是等腰三角形,通过解直角三角形得出C′C″=10
.就可求得△CDE的周长的最小值.
| 3 |
解答: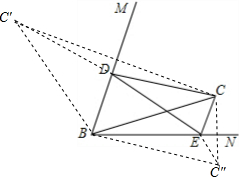 解:分别作点C关于BM、BN的对称点C′、C″,连接C′C″,分别交BM、BN于点D、E,连接BC′、BC″.
解:分别作点C关于BM、BN的对称点C′、C″,连接C′C″,分别交BM、BN于点D、E,连接BC′、BC″.
∵点C关于BM的对称点C′,
∴DC=DC′,BC=BC′,∠C′BM=∠CBM;
∵点C关于BN的对称点为C″,
∴EC=EC″,BC=BC″,∠NBC″=∠NBC,
∴BC′=BC″=OC=10,∠C′BC″=120°,
∴△C′BC″是等腰三角形,
∴C′C″=10
.
∴△CDE的周长的最小值=CD+MDE+CE=DC′+DE+DEC″≥CD=10
.
故答案为10
.
 解:分别作点C关于BM、BN的对称点C′、C″,连接C′C″,分别交BM、BN于点D、E,连接BC′、BC″.
解:分别作点C关于BM、BN的对称点C′、C″,连接C′C″,分别交BM、BN于点D、E,连接BC′、BC″.∵点C关于BM的对称点C′,
∴DC=DC′,BC=BC′,∠C′BM=∠CBM;
∵点C关于BN的对称点为C″,
∴EC=EC″,BC=BC″,∠NBC″=∠NBC,
∴BC′=BC″=OC=10,∠C′BC″=120°,
∴△C′BC″是等腰三角形,
∴C′C″=10
| 3 |
∴△CDE的周长的最小值=CD+MDE+CE=DC′+DE+DEC″≥CD=10
| 3 |
故答案为10
| 3 |
点评:此题主要考查轴对称--最短路线问题,轴对称的性质,等腰三角形的判定和性质,解直角三角形等,综合运用了等腰三角形的知识是本题的关键.

练习册系列答案
相关题目
 在∠AOB的内部从顶点O引出3条射线,则图中共有角的个数是( )
在∠AOB的内部从顶点O引出3条射线,则图中共有角的个数是( )| A、9个 | B、10个 |
| C、11个 | D、12个 |
下列事件中,是必然事件的是( )
| A、掷3次一枚质地均匀的硬币,必有1次有字的一面朝上 |
| B、买一张福利彩票一定中大奖 |
| C、若a,b为实数,则a•b=b•a |
| D、平面内,梯形的对边一定平行 |
 如图所示,∠BAF,∠CBD,∠ACE是△ABC的三个外角,求∠BAF+∠CBD+∠ACE的度数.
如图所示,∠BAF,∠CBD,∠ACE是△ABC的三个外角,求∠BAF+∠CBD+∠ACE的度数. 如图,完成下列填空:
如图,完成下列填空: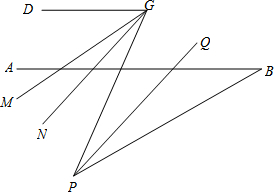 如图,在(1)的结论下,AB的下方点P满足∠ABP=30°,G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP-∠MGN的值不变;②∠MGN的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值.
如图,在(1)的结论下,AB的下方点P满足∠ABP=30°,G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP-∠MGN的值不变;②∠MGN的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值. 如图,在正方形ABCD中,OE=OF.求证:
如图,在正方形ABCD中,OE=OF.求证: 如图,是一个圆心人工湖的平面图,弦AB是湖上的一座桥,已知桥长100m,测得圆周角∠ACB=30°,则这个人工湖的直径为
如图,是一个圆心人工湖的平面图,弦AB是湖上的一座桥,已知桥长100m,测得圆周角∠ACB=30°,则这个人工湖的直径为