题目内容
5.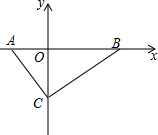 如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,顶点C在y轴的负半轴上,tan∠ABC=$\frac{3}{4}$,点P在线段OC上,且PO、PC的长(P0<PC)是x2-12x+27=0的两根.
如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,顶点C在y轴的负半轴上,tan∠ABC=$\frac{3}{4}$,点P在线段OC上,且PO、PC的长(P0<PC)是x2-12x+27=0的两根.(1)求P点坐标;
(2)若∠ACB的平分线交x轴于点D,求直线CD的解析式;
(3)若M是射线CD上的点,在平面内是否存在点Q,使以A、C、M、Q为顶点的四边形是矩形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
分析 (1)由PO、PC的长(P0<PC)是x2-12x+27=0的两根,解方程可得出PO=3,结合点P在线段OC上可得出P点的坐标;
(2)由(1)可得出OC的长,结合tan∠ABC=$\frac{3}{4}$在直角三角形COB中可求出OB的长度,由∠CAB与∠ABC互余可得出cot∠BAC=tan∠ABC,在直角三角形AOC中可求出AO的长度,从而得出B、A点的坐标,结合C点的坐标可找出直线AC、BC的解析式,由CD平分∠ACB可得出点D到直线AC的距离等于点D到直线BC的距离,设出D点坐标,由点到直线的距离即可得出关于m的一元一次方程,解方程即可得出D点坐标,结合C点坐标即可得出直线CD的解析式;
(3)结合∠ACB=90°可知点Q在直线BC上,由CD平分∠ACB,可得出以A、C、M、Q为顶点的四边形是正方形,设出Q点坐标,由CQ=AC即可得出结论.
解答 解:(1)∵PO、PC的长(P0<PC)是x2-12x+27=0的两根,
∴PO=3,PC=9.
又∵点P在线段OC上,
∴点P的坐标为(0,-3).
(2)∵PO=3,PC=9,
∴OC=OP+PC=12,
∴点C的坐标为(0,-12)
在Rt△COB中,tan∠ABC=$\frac{3}{4}$,OC=12,
∴OB=$\frac{OC}{tan∠ABC}$=16,
∴点B的坐标为(0,16).
∵△ABC为直角三角形,
∴cot∠BAC=tan∠ABC=$\frac{3}{4}$,
在Rt△AOC中,cot∠OAC=$\frac{3}{4}$,OC=12,
∴OA=OC•cot∠OAC=9,
∴点A的坐标为(-9,0).
∴直线BC的解析式为y=$\frac{3}{4}$x-12,即$\frac{3}{4}$x-y-12=0;
直线AC的解析式为y=-$\frac{4}{3}$x-12,即$\frac{4}{3}$x+y+12=0.
设点D的坐标为(m,0).
∵点D为∠ACB的平分线上的点,
∴有$\frac{|\frac{3}{4}m-12|}{\sqrt{(\frac{3}{4})^{2}+(-1)^{2}}}$=$\frac{|\frac{4}{3}m+12|}{\sqrt{(\frac{4}{3})^{2}+{1}^{2}}}$,
解得:m=$\frac{12}{7}$,
故点D的坐标为($\frac{12}{7}$,0),
直线CD的解析式为y=7x-12.
(3)假设存在,画出图形如下.
∵以A、C、M、Q为顶点的四边形是矩形,
∴点Q在直线BC上,
∵CD为∠ACD的角平分线,
∴∠ACM=45°,
∴AM=AC=CQ=MQ.
设点Q的坐标为(x,$\frac{3}{4}$x-12).
∵AC=$\sqrt{1{2}^{2}+{9}^{2}}$=15,CQ=$\sqrt{{x}^{2}+(\frac{3}{4}x-12+12)^{2}}$,
∴$\sqrt{{x}^{2}+(\frac{3}{4}x-12+12)^{2}}$=15,
解得:x=12,或x=-12(舍去),
即点Q的坐标为(12,-3).
故在平面内存在点Q,使以A、C、M、Q为顶点的四边形是矩形,点Q的坐标为(12,-3).
点评 本题考查了解一元二次方程、利用三角函数值解直角三角形、点到直线的距离以及正方形的判定及性质,解题的关键:(1)解一元二次方程;(2)利用点到直线的距离找出关于m的一元一次方程;(3)正方形的判定及性质.本题属于中档题,难度不大,(1)难度很小;(2)借助了角平分线的性质与点到直线的距离公式列出方程;(3)结合图形与已知找出以A、C、M、Q为顶点的四边形是正方形.

| A. | m2+n2=(m+n)(m-n) | B. | x2+2x-1=(x-1)2 | C. | a2-a=a(a-1) | D. | a2+2a+1=a(a+2)+1 |
| A. | m=±1 | B. | m=1 | C. | m=±$\sqrt{3}$ | D. | m=-1 |
| A. | $\sqrt{25}$=5 | B. | ±$\sqrt{64}$=±8 | C. | $\sqrt{(-6)^{2}}$=-6 | D. | $\root{3}{-8}$=-2 |
 已知:如图,在直角梯形纸片ABCD中,DC∥AB,AB>CD>AD,∠A=90°,将纸片沿过点D的直线翻折,使点A落在边CD上的点E处,折痕为DF,联结EF并展开纸片.
已知:如图,在直角梯形纸片ABCD中,DC∥AB,AB>CD>AD,∠A=90°,将纸片沿过点D的直线翻折,使点A落在边CD上的点E处,折痕为DF,联结EF并展开纸片.