题目内容
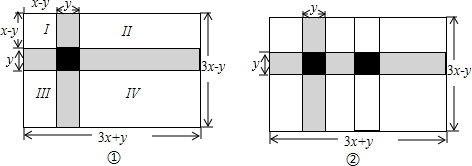
去年,某校为提升学生综合素质推出一系列校本课程,“蔬菜种植课”上张老师用两条宽均为y 米的小道将一块长(3x+y)米、宽(3x-y)米的长方形土地分成Ⅰ、Ⅱ、Ⅲ、Ⅳ部分(如图①的形状).
(1)求图①中小道的面积并化简;
(2)由于去年学生报名人数有限,张老师只要求学生们在Ⅰ部分土地上种植A型蔬菜,在Ⅳ部分土地上种植B型蔬菜.已知种植A型蔬菜每平方米的产量是6千克,种植B型蔬菜每平方米的产量是4千克.求去年种植蔬菜的总产量并化简;
(3)今年“蔬菜种植课”反响热烈,有更多学生报名参加.张老师不得不将该土地分成如图②的形状,并全部种上B型蔬菜.如果今年B型蔬菜的产量与去年一样,那么今年蔬菜总产量比去年多多少千克?(结果要化简)
(1)求图①中小道的面积并化简;
(2)由于去年学生报名人数有限,张老师只要求学生们在Ⅰ部分土地上种植A型蔬菜,在Ⅳ部分土地上种植B型蔬菜.已知种植A型蔬菜每平方米的产量是6千克,种植B型蔬菜每平方米的产量是4千克.求去年种植蔬菜的总产量并化简;
(3)今年“蔬菜种植课”反响热烈,有更多学生报名参加.张老师不得不将该土地分成如图②的形状,并全部种上B型蔬菜.如果今年B型蔬菜的产量与去年一样,那么今年蔬菜总产量比去年多多少千克?(结果要化简)

考点:整式的混合运算
专题:应用题
分析:(1)利用已知图形进而得出两条小道的面积之和即可;
(2)利用已知图形进而得出去年蔬菜的总产量即可;
(3)首先求出今年蔬菜总产量,进而得出答案.
(2)利用已知图形进而得出去年蔬菜的总产量即可;
(3)首先求出今年蔬菜总产量,进而得出答案.
解答:解:(1)两条小道的面积之和:y(3x+y)+y(3x-y)-y2=(6xy-y2)平方米;
(2)去年蔬菜的总产量:
6(x-y)2+4[(3x+y)-2y]•[(3x-y)-y]
=(22x2-12xy+2y2)千克;
(3)今年蔬菜总产量:4[(3x+y)-2y]•[(3x-y)-y]=(36x2-48xy+8y2)千克,
今年蔬菜总产量比去年多:
(36x2-48xy+8y2)-(22x2-12xy+2y2)
=(14x2-36xy+6y2)千克.
(2)去年蔬菜的总产量:
6(x-y)2+4[(3x+y)-2y]•[(3x-y)-y]
=(22x2-12xy+2y2)千克;
(3)今年蔬菜总产量:4[(3x+y)-2y]•[(3x-y)-y]=(36x2-48xy+8y2)千克,
今年蔬菜总产量比去年多:
(36x2-48xy+8y2)-(22x2-12xy+2y2)
=(14x2-36xy+6y2)千克.
点评:此题主要考查了整式的混合运算,正确利用图形求出是解题关键.

练习册系列答案
相关题目
下列各式按字母x的降幂排列的是( )
| A、-5x2-x2+2x2 |
| B、ax3-2bx+cx2 |
| C、-x2y-2xy2+y2 |
| D、x2y-3xy2+x3-2y2 |
若一元二次方程x2-2x-7=0的两根是x1和x2,则x1+x2-x1x2的值是( )
| A、10 | B、9 | C、7 | D、8 |
 如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.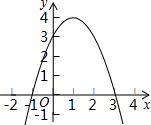 已知二次函数y=-x2+2x+k+2与x轴的公共点有两个.求:
已知二次函数y=-x2+2x+k+2与x轴的公共点有两个.求: