题目内容
18.下列运算正确的个数是( )①2a2-a2=a2;
②$\sqrt{2}$+$\sqrt{4}$=2$\sqrt{2}$;
③(π-3.14)0×$\sqrt{3}$=0;
④a2÷a×$\frac{1}{a}$=a2;
⑤sin30°+cos60°=$\frac{1+\sqrt{3}}{2}$;
⑥精确到万位6295382≈6.30×106.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据合并同类项,二次根式的加减,零次幂,分化式的乘除,特殊角三角函数值,近似数,可得答案.
解答 解:①2a2-a2=a2;
②$\sqrt{2}$+$\sqrt{4}$=2+$\sqrt{2}$,故②错误;
③(π-3.14)0×$\sqrt{3}$=$\sqrt{3}$,故③错误;
④a2÷a×$\frac{1}{a}$=1,故④错误;
⑤sin30°+cos60°=1,故⑤错误;
⑥精确到万位6295382≈6.30×106,故⑥正确;
故选:B.
点评 本题考查考了合并同类项,二次根式的加减,零次幂,分化式的乘除,特殊角三角函数值,近似数,熟记法则并根据法则计算是解题关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
8.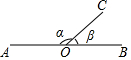 如图,O为直线AB上一点,∠AOC=α,∠BOC=β,则β的余角可表示为( )
如图,O为直线AB上一点,∠AOC=α,∠BOC=β,则β的余角可表示为( )
 如图,O为直线AB上一点,∠AOC=α,∠BOC=β,则β的余角可表示为( )
如图,O为直线AB上一点,∠AOC=α,∠BOC=β,则β的余角可表示为( )| A. | $\frac{1}{2}$(α+β) | B. | $\frac{1}{2}$α | C. | $\frac{1}{2}$(α-β) | D. | $\frac{1}{2}$β |
9.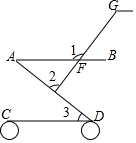 如图所示是婴儿车的平面示意图,其中AB∥CD,∠1=121°,∠3=42°,那么∠2的度数为( )
如图所示是婴儿车的平面示意图,其中AB∥CD,∠1=121°,∠3=42°,那么∠2的度数为( )
 如图所示是婴儿车的平面示意图,其中AB∥CD,∠1=121°,∠3=42°,那么∠2的度数为( )
如图所示是婴儿车的平面示意图,其中AB∥CD,∠1=121°,∠3=42°,那么∠2的度数为( )| A. | 79° | B. | 89° | C. | 59° | D. | 91° |
6.运用乘法公式计算(4+x)(4-x)的结果是( )
| A. | x2-16 | B. | 16-x2 | C. | x2+16 | D. | x2-8x+16 |
13.3-$\sqrt{5}$的绝对值是( )
| A. | 3-$\sqrt{5}$ | B. | $\sqrt{5}$-3 | C. | -3-$\sqrt{5}$ | D. | 3+$\sqrt{5}$ |
5.在平面直角坐标系中,将抛物线C1:y=x2平移后得到抛物线C2,使得抛物线C2恰好经过抛物线C1的顶点,且抛物线C2与x轴有两个交点,分别记为点A、点B.若AB=2$\sqrt{3}$,抛物线C2的顶点为点C,则△ABC的周长是( )
| A. | 3+2$\sqrt{2}$ | B. | 6+2$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 12$\sqrt{3}$ |