题目内容
9．
如图，四边形ABCD是⊙O的内接四边形，若∠BOD=88°，则∠BCD的度数是136°．
分析 根据圆周角定理求出∠A的度数，根据圆内接四边形计算即可．
解答 解：由圆周角定理得，∠A=$\frac{1}{2}$∠BOD=44°，
由圆内接四边形的性质得，∠BCD=180°-∠A=136°，
故答案为：136°．
点评 本题考查的是圆周角定理和圆内接四边形的性质，掌握圆内接四边形的对角互补、同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
某校对学生上学方式进行了一次抽样调查，并根据此次调查结果绘制了一个不完整的扇形统计图，其中“其他”部分所对应的圆心角是36°，则“步行”部分所占百分比是40%．
17．
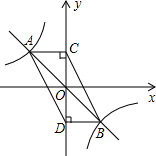如图，正比例函数y=-x与反比例函数y=-$\frac{2}{x}$的图象相交于A、B两点，分别过A、B两点作y轴的垂线，垂足分别为C、D，连接AD，BC，则四边形ACBD的面积为（ ）
如图，正比例函数y=-x与反比例函数y=-$\frac{2}{x}$的图象相交于A、B两点，分别过A、B两点作y轴的垂线，垂足分别为C、D，连接AD，BC，则四边形ACBD的面积为（ ）| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
4．如果把分式$\frac{2xy}{x+y}$中的x和y都扩大2倍，那么分式的值（ ）
| A． | 扩大为原来的4倍 | B． | 扩大为原来的2倍 | ||
| C． | 不变 | D． | 缩小为原来的$\frac{1}{2}$倍 |
14．下列因式分解错误的是（ ）
| A． | x2-y2=（x+y）（x-y） | B． | x2+y2=（x+y）2 | C． | x2+xy=x（x+y） | D． | x2+6x+9=（x+3）2 |
1．下列图形中，是中心对称图形但不是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |