Question

8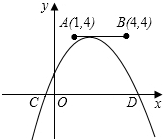．如图，点A，B的坐标分别为（1，4）和（4，4），抛物线y=a（x-m）²+n的顶点在线段AB上运动，与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为-3，则点D的横坐标最大值为（　　）

• A． 13
• B． 7
• C． 5
• D． 8

Answer 1

分析 当C点横坐标最小时，抛物线顶点必为A（1，4），根据此时抛物线的对称轴，可判断出CD间的距离；
当D点横坐标最大时，抛物线顶点为B（4，4），再根据此时抛物线的对称轴及CD的长，可判断出D点横坐标最大值．

解答 解：当点C横坐标为-3时，抛物线顶点为A（1，4），对称轴为x=1，此时D点横坐标为5，则CD=8；
当抛物线顶点为B（4，4）时，抛物线对称轴为x=4，且CD=8，故C（0，0），D（8，0）；
由于此时D点横坐标最大，
故点D的横坐标最大值为8．
故选D．

点评 本题主要考查了二次函数的性质，能够正确地判断出点C横坐标最小、点D横坐标最大时抛物线的顶点坐标是解答此题的关键．