题目内容
6.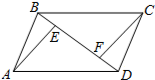 如图,AB∥CD,BC∥AD,AB=CD,BE=DF,图中全等的三角形的对数是( )
如图,AB∥CD,BC∥AD,AB=CD,BE=DF,图中全等的三角形的对数是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据平行线的性质求出∠ABD=∠CDB,∠ADB=∠CBD,根据ASA推出△ABD≌△CDB,根据全等三角形的对应边相等得出AD=BC,AB=CD,再根据SAS推出△ABE≌△CDF,根据全等三角形的对应边相等得出AE=CF,求出BF=DE,根据SSS推出△ADE≌△CBF即可.
解答  解:∵AB∥CD,BC∥AD,
解:∵AB∥CD,BC∥AD,
∴∠ABD=∠CDB,∠ADB=∠CBD.
在△ABD和△CDB中
$\left\{\begin{array}{l}{∠ABD=∠CDB}\\{BD=DB}\\{∠ADB=∠CBD}\end{array}\right.$,
∴△ABD≌△CDB(ASA),
∴AD=BC,AB=CD.
在△ABE和△CDF中
$\left\{\begin{array}{l}{AB=CD}\\{∠ABE=∠CDF}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△CDF(SAS),
∴AE=CF.
∵BE=DF,
∴BE+EF=DF+EF,
∴BF=DE,
在△ADE和△CBF中
$\left\{\begin{array}{l}{AD=CB}\\{DE=BF}\\{AE=CF}\end{array}\right.$,
∴△ADE≌△CBF(SSS),
即3对全等三角形,
故选A.
点评 本题考查了平行线的性质,全等三角形的性质和判定的应用,能正确根据定理进行推理是解此题的关键,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
14.小明在假期里参加四天一期的夏令营活动,这四天各天的日期和为66,则夏令营的开营日( )
| A. | 15日 | B. | 16日 | C. | 17日 | D. | 18日 |
1.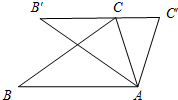 如图,把△ABC绕着点A顺时针方向旋转34°,得到△AB′C′,点C刚好落在边B′C′上.则∠C′=( )
如图,把△ABC绕着点A顺时针方向旋转34°,得到△AB′C′,点C刚好落在边B′C′上.则∠C′=( )
 如图,把△ABC绕着点A顺时针方向旋转34°,得到△AB′C′,点C刚好落在边B′C′上.则∠C′=( )
如图,把△ABC绕着点A顺时针方向旋转34°,得到△AB′C′,点C刚好落在边B′C′上.则∠C′=( )| A. | 56° | B. | 62° | C. | 68° | D. | 73° |
11.下列计算结果为负数的是( )
| A. | -(-2)3 | B. | -(-2)4 | C. | (-1)-(-3) | D. | 16÷(-4)2 |
18.下表为北京市居民每月用水收费标准,(单位:元/m3).
(1)某用户用水4立方米,共交水费20元,求a的值;
(2)在(1)的条件下,该用户12月份交水费89元,请问该用户12月份用水多少立方米?
| 用水量(m3) | 单价 |
| 0-15 | a |
| 15.1-21.7 | a+2 |
| 21.8以上 | a+4 |
(2)在(1)的条件下,该用户12月份交水费89元,请问该用户12月份用水多少立方米?