题目内容
6.若a+b=5,ab=2,求$\frac{1}{2}$a3b+a2b2+$\frac{1}{2}$ab3的值.分析 先把代数式利用提公因式法、完全平方公式进行分解因式,然后再代入求值即可解答.
解答 解:$\frac{1}{2}$a3b+a2b2+$\frac{1}{2}$ab3
=$\frac{1}{2}$ab(a2+2ab+b2)
=$\frac{1}{2}$ab(a+b)2
当a+b=5,ab=2时,原式=$\frac{1}{2}×2×{5}^{2}$=25.
点评 本题考查了因式分解的应用,解决本题的关键是利用提公因式法和完全平方公式进行因式分解.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
16.计算(-a)2a3的结果有( )
| A. | a6 | B. | -a6 | C. | -a5 | D. | a5 |
1.已知等腰三角形的一边长是10m,面积是30m2,则这个三角形另两边的长为$\sqrt{61}$m、$\sqrt{61}$m或10m、2$\sqrt{10}$m或10m、6$\sqrt{10}$m.
18.已知$\left\{\begin{array}{l}{2a-3b+4c=0}\\{3a-4b+5c=0}\end{array}\right.$,则a:b:c=( )
| A. | 1:2:3 | B. | 1:2:1 | C. | 1:3:1 | D. | 3:2:1 |
16. 如图中的两个三角形全等,则∠1=( )
如图中的两个三角形全等,则∠1=( )
 如图中的两个三角形全等,则∠1=( )
如图中的两个三角形全等,则∠1=( )| A. | 45° | B. | 58° | C. | 76° | D. | 77° |
 如图,点G是△ABC的重心,过点G作EF∥BC,分别交AB、AC于点E、F,且EF+BC=7.2cm,求BC的长.
如图,点G是△ABC的重心,过点G作EF∥BC,分别交AB、AC于点E、F,且EF+BC=7.2cm,求BC的长.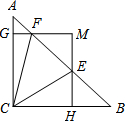 在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;其中正确结论为①②.
在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;其中正确结论为①②.