题目内容
11.实数x,y满足5x2+2y2-2xy-2x-2y+1=0,则x2+y2=$\frac{5}{9}$.分析 首先将5x2+2y2-2xy-2x-2y+1=0转化为(2x-y)2+(x+y-1)2=0,然后利用非负数的性质,求出x、y的值,再应用代入法,求出x2+y2的值是多少即可.
解答 解:∵5x2+2y2-2xy-2x-2y+1=0,
∴(4x2+y2-4xy)+(x2+y2+2xy-2x-2y+1)=0,
∴(2x-y)2+(x+y-1)2=0,
∴$\left\{\begin{array}{l}{2x-y=0}\\{x+y-1=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{2}{3}}\end{array}\right.$
∴x2+y2=${(\frac{1}{3})}^{2}$+${(\frac{2}{3})}^{2}$=$\frac{5}{9}$.
故答案为:$\frac{5}{9}$.
点评 此题主要考查了因式分解的应用,以及非负数的性质的应用,要熟练掌握.

练习册系列答案
相关题目
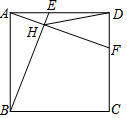 如图,正方形ABCD的边AD、CD上两个动点E,F,且满足AF=BE,BE交AF于点H.若正方形的边长为4,线段DH最大值为x,最小值为y,则$\sqrt{x}$-y的值是4-2$\sqrt{5}$.
如图,正方形ABCD的边AD、CD上两个动点E,F,且满足AF=BE,BE交AF于点H.若正方形的边长为4,线段DH最大值为x,最小值为y,则$\sqrt{x}$-y的值是4-2$\sqrt{5}$. 如图,AE⊥EF于点E,BF⊥EF于点F,连接AB交EF于点D.在线段AB上取一点C,使EB=EC=AC,若∠EBF=54°,则∠ABF=18°.
如图,AE⊥EF于点E,BF⊥EF于点F,连接AB交EF于点D.在线段AB上取一点C,使EB=EC=AC,若∠EBF=54°,则∠ABF=18°. 如图,在四边形ABCD中,AD∥BC,对角线AC⊥BD,若AD=6,BC=14,则四边形ABCD面积的最大值是100.
如图,在四边形ABCD中,AD∥BC,对角线AC⊥BD,若AD=6,BC=14,则四边形ABCD面积的最大值是100.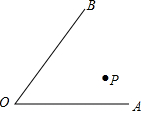 如图,∠AOB内有一点P
如图,∠AOB内有一点P