题目内容
12．
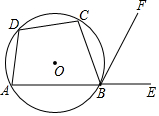如图，ABCD是⊙O的内接四边形，点E在AB的延长线上，BF是∠CBE的平分线，∠ADC=110°，则∠FBE=55°．
分析 根据圆内接四边形的性质求出∠CBE=∠ADC=110°，根据角平分线定义求出即可．
解答 解：∵ABCD是⊙O的内接四边形，∠ADC=110°，
∴∠CBE=∠ADC=110°，
∵BF是∠CBE的平分线，
∴∠FBE=$\frac{1}{2}$∠CBE=55°，
故答案为：55°．
点评 本题考查了圆内接四边形性质的应用，能求出∠CBE=∠ADC是解此题的关键．
练习册系列答案
相关题目
2．在直角坐标系中与（2，-3）在同一个正比例函数图象上的是（ ）
| A． | （2，3） | B． | （-2，-3） | C． | （4，-6） | D． | （-4，-6） |
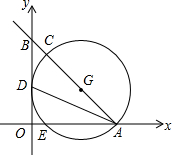如图，在直角坐标系中，直线AB与x、y轴分别交于点A（4，0）、B（0，$\frac{16}{3}$）两点，∠BAO的角平分线交y轴于点D，点C为直线AB上一点以AC为直径的⊙G经过点D，且与x轴交于另一点E．
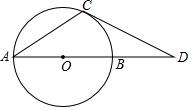如图，AB是⊙O的直径，DC是⊙O相切于点C，若∠D=30°，OA=2，则CD=2$\sqrt{3}$．
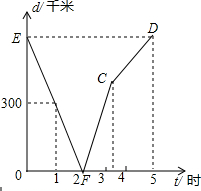甲、乙两列火车分别从A，B两城同时相向匀速驶出，甲车开往终点B城，乙车开往终点A城，乙车比甲车早到达终点；如图，是两车相距的路程d（千米）与行驶时间t（小时）的函数关系图象．
用8块相同的长方形地砖拼成一块矩形地面，地砖的拼放方式及相关数据如图所示，求每块地砖的长与宽．