题目内容
7.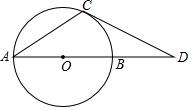 如图,AB是⊙O的直径,DC是⊙O相切于点C,若∠D=30°,OA=2,则CD=2$\sqrt{3}$.
如图,AB是⊙O的直径,DC是⊙O相切于点C,若∠D=30°,OA=2,则CD=2$\sqrt{3}$.
分析 直接利用切线的性质得出∠OCD=90°,进而勾股定理得出DC的长.
解答  解:连接CO,
解:连接CO,
∵DC是⊙O相切于点C,
∴∠OCD=90°,
∵∠D=30°,OA=CO=2,
∴DO=4,
∴CD=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 此题主要考查了切线的性质以及勾股定理,正确得出DO的长是解题关键.

练习册系列答案
相关题目
17.若∠P=25°12′,∠Q=25.12°,∠R=25.2°,则下列结论正确的是( )
| A. | ∠P=∠Q | B. | ∠P=∠R | C. | ∠Q=∠R | D. | ∠P=∠Q=∠R |
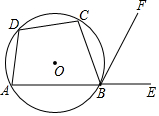 如图,ABCD是⊙O的内接四边形,点E在AB的延长线上,BF是∠CBE的平分线,∠ADC=110°,则∠FBE=55°.
如图,ABCD是⊙O的内接四边形,点E在AB的延长线上,BF是∠CBE的平分线,∠ADC=110°,则∠FBE=55°.