题目内容
1.已知实数x、y满足|y-$\sqrt{3}$|+$\sqrt{x-4}$=0,则xy=4$\sqrt{3}$.分析 先根据非负数的性质求出x,y的值,进而可得出结论.
解答 解:∵实数x、y满足|y-$\sqrt{3}$|+$\sqrt{x-4}$=0,
∴y-$\sqrt{3}$=0,x-4=0,解得y=$\sqrt{3}$,x=4,
∴xy=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查的是非负数的性质,熟知算术平方根与绝对值具有非负性是解答此题的关键.

练习册系列答案
相关题目
9.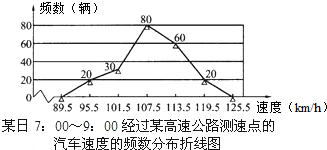 超速行驶是交通事故频发的主要原因之一,交警部门统计某日7:00-9:00经过高速公路某测速点的汽车的速度,得到如下频数分布折线图,若该路段汽车限速110km/h,则超速行驶的汽车有( )
超速行驶是交通事故频发的主要原因之一,交警部门统计某日7:00-9:00经过高速公路某测速点的汽车的速度,得到如下频数分布折线图,若该路段汽车限速110km/h,则超速行驶的汽车有( )
 超速行驶是交通事故频发的主要原因之一,交警部门统计某日7:00-9:00经过高速公路某测速点的汽车的速度,得到如下频数分布折线图,若该路段汽车限速110km/h,则超速行驶的汽车有( )
超速行驶是交通事故频发的主要原因之一,交警部门统计某日7:00-9:00经过高速公路某测速点的汽车的速度,得到如下频数分布折线图,若该路段汽车限速110km/h,则超速行驶的汽车有( )| A. | 20辆 | B. | 60辆 | C. | 70辆 | D. | 80辆 |
6.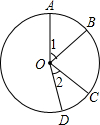 如图,在⊙O中,$\widehat{AB}$=$\widehat{CD}$,∠1=45°,则∠2=( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{CD}$,∠1=45°,则∠2=( )
 如图,在⊙O中,$\widehat{AB}$=$\widehat{CD}$,∠1=45°,则∠2=( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{CD}$,∠1=45°,则∠2=( )| A. | 60° | B. | 30° | C. | 45° | D. | 40° |
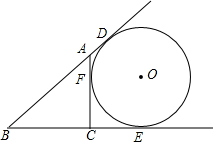 如图所示,已知AC⊥BC,BC=4,AC=3,⊙O与直线AB,BC,CA都相切,切点分别为D,E,F.求⊙O的半径.
如图所示,已知AC⊥BC,BC=4,AC=3,⊙O与直线AB,BC,CA都相切,切点分别为D,E,F.求⊙O的半径.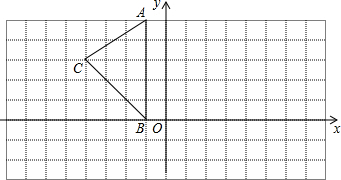 如图,在平面直角坐标系中
如图,在平面直角坐标系中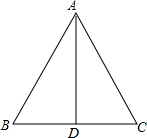 如图,AD为△ABC中∠BAC的角平分线,且BD=DC,试判断线段AB与AC的关系,并给予证明.
如图,AD为△ABC中∠BAC的角平分线,且BD=DC,试判断线段AB与AC的关系,并给予证明.