题目内容
11.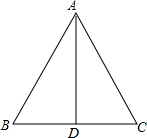 如图,AD为△ABC中∠BAC的角平分线,且BD=DC,试判断线段AB与AC的关系,并给予证明.
如图,AD为△ABC中∠BAC的角平分线,且BD=DC,试判断线段AB与AC的关系,并给予证明.
分析 过点D分别作AB、AC的垂线,垂足分别为E、F,证明△AED与△AFD全等,再进而证明即可.
解答 解:AB=AC,理由如下:
过点D分别作AB、AC的垂线,垂足分别为E、F,
∵AD为△ABC中∠BAC的角平分线,
∴ED=FD,
在△AED与△AFD中,
$\left\{\begin{array}{l}{AD=AD}\\{∠EAD=∠FAD}\\{DE=DF}\end{array}\right.$,
∴△AED≌△AFD(SAS),
∴AE=AF,
在Rt△BED与Rt△DFC中,
$\left\{\begin{array}{l}{ED=FD}\\{BD=DC}\end{array}\right.$,
∴Rt△BED≌Rt△DFC(HL),
∴EB=FC,
∴AB=AC.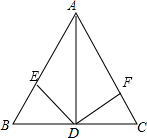
点评 此题考查全等三角形的判定和性质,关键是证明△AED与△AFD全等.

练习册系列答案
相关题目
19.下列说法错误的是( )
| A. | 5是25的算术平方根 | B. | $\frac{5}{6}$是$\frac{25}{36}$的一个平方根 | ||
| C. | (-4)2的平方根是-4 | D. | 0的平方根与算术平方根都是0 |
3.下列各式从左到右的变形中,是因式分解的是( )
| A. | (a+3)(a-3)=a2-9 | B. | m2-m+2=m(m-1+$\frac{2}{m}$) | C. | a2-4a-5=a(a-4)-5 | D. | a2-4a+4=(a-2)2 |
17.一位鞋店的经理,为了解鞋子的销售情况,随机调查了一个月销售的鞋子的尺码,对这组数据的分析中,鞋店的经理最感兴趣的是这组数据的( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
 如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C,D是垂足,连接CD,与∠AOB的平分线交于点F,
如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C,D是垂足,连接CD,与∠AOB的平分线交于点F,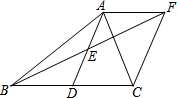 如图,在△ABC中,D是BC的中点,E是AD的中点,过A点作BC的平行线交BE的延长线于F,连接CF.
如图,在△ABC中,D是BC的中点,E是AD的中点,过A点作BC的平行线交BE的延长线于F,连接CF.