题目内容
(本题满分12分)如图,抛物线 与x轴交于点A(1,0)和B(3,0).
与x轴交于点A(1,0)和B(3,0).

(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;
(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1)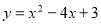 ;(2)C(4,3);(3)P(
;(2)C(4,3);(3)P(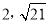 )或(
)或(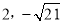 )或(
)或( )或(
)或(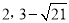 ).
).
【解析】
试题分析:(1)把点A、B的坐标代入函数解析式,解方程组求出a、b的值,即可得解;
(2)根据抛物线解析式求出对称轴,再根据平行四边形的对角线互相平分求出点C的横坐标,然后代入函数解析式计算求出纵坐标,即可得解;
(3)设AC、EF的交点为D,根据点C的坐标写出点D的坐标,然后分①O是顶角,②C是顶角,③P是顶角三种情况讨论.
试题解析:(1)把点A(1,0)和B(3,0)代入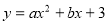 得,
得,
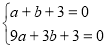 ,解得
,解得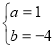 ,所以,抛物线的解析式为
,所以,抛物线的解析式为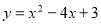 ;
;
(2)抛物线的对称轴为直线x=2,
∵四边形OECF是平行四边形∴点C的横坐标是4,
∵点C在抛物线上,∴ ,
,
∴点C的坐标为(4,3);
(3)∵点C的坐标为(4,3),∴OC的长为5,
①点O是顶角顶点时,OP=OC=5,
∵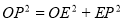 ,OE=2∴
,OE=2∴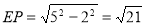 ,
,
所以,点P的坐标为(2,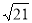 )或(2,-
)或(2,-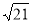 );
);
②点C是顶角顶点时,CP=OC=5,同理求出PF=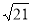 ,所以,PE=
,所以,PE=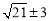 ,
,
所以,点P的坐标为(2,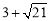 )或(2,
)或(2, 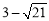 );
);
③点P是顶角顶点时,点P在OC上,不存在.
综上所述,抛物线的对称轴上存在点P(2,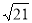 )或(2,-
)或(2,-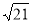 )或(2,
)或(2,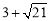 )或(2,
)或(2, 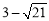 ),使△OCP是等腰三角形.
),使△OCP是等腰三角形.
考点:二次函数综合题.

练习册系列答案
相关题目
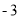 时,有最大值
时,有最大值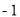 ,且当x=0时,y=
,且当x=0时,y= 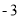 ,求二次函数的解析式。
,求二次函数的解析式。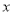 的一元二次方程
的一元二次方程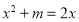 ,没有实数根,则实数
,没有实数根,则实数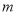 的取值范围是( )
的取值范围是( )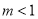 B.
B. 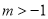 C.
C.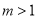 D.
D.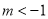

 向左平移1个单位,再向上平移3个单位得到的抛物线,其表达式为( )
向左平移1个单位,再向上平移3个单位得到的抛物线,其表达式为( ) B.
B.
 D.
D.
 ③;①③
③;①③ ②;②③
②;②③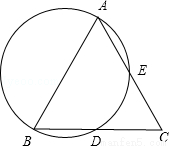
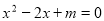 .
. ,
, ,且
,且 ,求m的值.
,求m的值.