Question

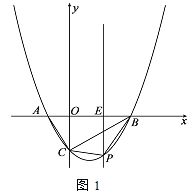
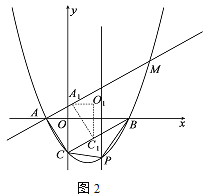
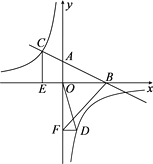
【题目】如图，在平面直角坐标系中，直线AB与x轴交于点B，与y轴交于点A，与反比例函数的图象在第二象限交于点C，CE⊥x轴，垂足为点E，，OB＝2，OE＝1．

（1）求反比例函数的解析式；

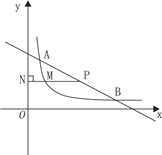
（2）若点D是反比例函数图象在第四象限上的点，过点D作DF⊥y轴，垂足为点F，连接OD、BF，如果SBAF＝4SDFO，求点D的坐标.

Answer 1

【答案】(l) y＝；(2) D（，-2）．

【解析】（1）由边的关系可得出BE=6，通过解直角三角形可得出CE=3，结合函数图象即可得出点C的坐标，再根据点C的坐标利用反比例函数图象上点的坐标特征，即可求出反比例函数系数m，由此即可得出结论；

（2）由点D在反比例函数在第四象限的图象上，设出点D的坐标为（n，-）（n＞0）．通过解直角三角形求出线段OA的长度，再利用三角形的面积公式利用含n的代数式表示出S△BAF，根据点D在反比例函数图形上利用反比例函数系数k的几何意义即可得出S△DFO的值，结合题意给出的两三角形的面积间的关系即可得出关于n的分式方程，解方程，即可得出n值，从而得出点D的坐标．

（1）∵OB=2，OE=1，

∴BE=OB+OE=3．

∵CE⊥x轴，

∴∠CEB=90°．

在Rt△BEC中，∠CEB=90°，BE=3，sin∠ABO=，

∴tan∠ABO=，

∴CE=BEtan∠ABO=3×=，

结合函数图象可知点C的坐标为（-1，）．

∵点C在反比例函数y=的图象上，

∴k=-1×=-，

∴反比例函数的解析式为y=-．

（2）∵点D在反比例函数y=-第四象限的图象上，

∴设点D的坐标为（n，-）（n＞0）．

在Rt△AOB中，∠AOB=90°，OB=4，tan∠ABO=，

∴OA=OBtan∠ABO=2×=1．

∵S△BAF=AFOB=（OA+OF）OB=（1+）×2=1+．

∵点D在反比例函数y=-第四象限的图象上，

∴S△DFO=×|-|=．

∵S△BAF=4S△DFO，

∴1+=4×，

解得：n=，

经验证，n=是分式方程的解，

∴点D的坐标为（，-2）．